Свойства оценок
О.1.2. Оценка Q* параметра Q называется несмещенной, если ее математическое ожидание равно оцениваемому параметру Q при любом объеме выборки, то есть:
Если Замечание Если равенство
Несмещенная оценка Q* не всегда дает хорошее приближение оцениваемого параметра. В частности, возможные значения Q* могут быть сильно рассеяны вокруг своего среднего значения, то дисперсия D(Q*) может быть значительной. Очевидно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. По этой причине к статистической оценке предъявляется требование эффективности.
О.1.3. Оценка Q* называется эффективной, если при заданном объеме выборки n она имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема n к статистическим оценкам предъявляется требование состоятельности.
О.1.4. Оценка Q* параметра Q называется состоятельной, если для любого наперед заданного числа e > 0 вероятность В этом случае говорят, что Q* сходится к Q по вероятности. Из определения 1.4. следует, что если оценка Q* является состоятельной, то при достаточно больших n можно с вероятностью, близкой к 1, утверждать, что оценка Q* отличается от параметра Q меньше чем на e. Очевидно, что требованию состоятельности должна удовлетворять всякая оценка, пригодная для практического использования. Замечание Если оценка Q* параметра Q является несмещенной (то есть M(Q*) = Q) и при n ® ¥ ее дисперсия стремится к нулю (то есть D(Q*) ® 0 при n ® ¥), то оценка Q* является и состоятельной.
Вывод: В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, эффективности и состоятельности.
Вопрос 2. Оценка генеральной средней по выборочной средней
Пусть в результате независимых наблюдений над количественным признаком Х из генеральной совокупности извлечена выборка объема n со значениями признака x1, x2, …, xn. Пусть генеральная средняя В качестве оценки генеральной средней
1. Покажем, что
Будем рассматривать Тогда
Так как каждая из СВ Xi имеет то же распределение, что и генеральная совокупность, то заключаем, что числовые характеристики этих СВ и генеральной совокупности одинаковы. В частности,
Заменив в формуле (1) математическое ожидание а на
2. Покажем, что Так как Таким образом, при увеличении объема выборки n выборочная средняя
3. Эффективность или неэффективность оценки Вывод: Выборочная средняя
Вопрос 3. Оценка генеральной дисперсии по исправленной выборочной
Пусть в результате независимых наблюдений над количественным признаком Х из генеральной совокупности извлечена выборка объема n:
где Пусть генеральная дисперсия DГ неизвестна и требуется найти ее оценку по данным выборки. Если за оценку DГ принять выборочную дисперсию DВ, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что DВ является смещенной оценкой DГ, так как
Легко «исправить» выборочную дисперсию DВ так, чтобы М(DВ) было равно DГ. Достаточно для этого умножить DВ на дробь
Исправленная дисперсия s2 является несмещенной оценкой генеральной дисперсии DГ, так как
Замечание При достаточно больших значениях n объема выборки DВ и s2 различаются незначительно. На практике исправленной дисперсией s2 пользуются в том случае, если n < 30.
Вопрос 4. Доверительные интервалы. Точность оценки. Надежность
О.4.1. Оценка, которая определяется одним числом, называется точечной.
Рассмотренные ранее оценки При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
О.4.2. Оценка параметра Q называется интервальной, если она определяется двумя числами – концами интервала, который покрывает параметр Q.
Пусть Q* - оценка неизвестного параметра Q (Q - постоянное число, хотя Q может быть и СВ). Оценка Q* тем точнее определяет параметр Q, чем меньше |Q – Q*|. Другими словами, если e > 0 и
то чем меньше e, тем точнее оценка Q*. Число e называется точностью оценки Q*. Так как Q* - СВ, то и разность |Q – Q*| - СВ. Поэтому неравенство (2) при заданном e может выполняться только с некоторой вероятностью.
О.4.3. Надежностью (доверительной вероятностью) оценки Q* параметра Q для заданного e > 0 называется вероятность g, с которой осуществляется неравенство (2).
Замечание Обычно задается надежность g и определяется точность e.
Пусть Так как
то есть вероятность того, что интервал (Q*–e; Q*+e) заключает в себе (покрывает) неизвестный параметр Q, равна g.
О.4.4. Доверительным интервалом называется интервал (Q*–e; Q*+e), который покрывает неизвестный параметр Q с заданной надежностью g.
Замечание Границы доверительного интервала (Q*–e; Q*+e) находятся по выборке и поэтому являются СВ в отличие от оцениваемого параметра Q - величины неслучайной, поэтому правильнее говорить о том, что доверительный интервал «покрывает», а не «содержит» значение Q.
Метод доверительных интервалов разработал американский статистик Ю. Нейман на основе идей английского статистика Р. Фишера.
|

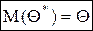
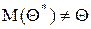 , то оценка Q* называется смещенной.
, то оценка Q* называется смещенной.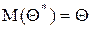 не выполняется, то оценка Q*, полученная по разным выборкам, будет в среднем либо завышать значение Q (
не выполняется, то оценка Q*, полученная по разным выборкам, будет в среднем либо завышать значение Q ( ), либо занижать его (
), либо занижать его (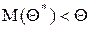 ), следовательно, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
), следовательно, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. при
при 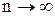 .
.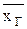 неизвестна и требуется найти ее оценку по данным выборки.
неизвестна и требуется найти ее оценку по данным выборки.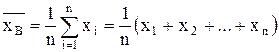 .
. - несмещенная оценка, то есть при любом объеме выборки n:
- несмещенная оценка, то есть при любом объеме выборки n: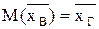 .
.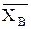 и значения
и значения 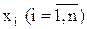 как независимые, одинаково распределенные СВ Xi. Так как СВ Xi распределены одинаково, то они имеют одинаковые числовые характеристики. В частности, M(Xi) = a для
как независимые, одинаково распределенные СВ Xi. Так как СВ Xi распределены одинаково, то они имеют одинаковые числовые характеристики. В частности, M(Xi) = a для 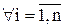 .
. (1)
(1) .
. , получим
, получим  , следовательно, несмещенность оценки
, следовательно, несмещенность оценки 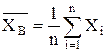 , то допуская, что СВ Xi имеют ограниченные дисперсии, применим к ним теорему Чебышева, в силу которой при n ® ¥ выборочная средняя
, то допуская, что СВ Xi имеют ограниченные дисперсии, применим к ним теорему Чебышева, в силу которой при n ® ¥ выборочная средняя 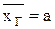 ).
). ,
,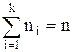 .
. .
.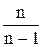 Þ сделав это, получим исправленную дисперсию:
Þ сделав это, получим исправленную дисперсию: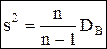
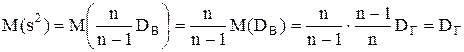
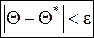 , (2)
, (2)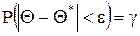 .
. Û
Û 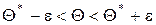 , то получим неравенство:
, то получим неравенство: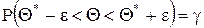 ,
,


