Внешняя характеристика трансформатора
При колебаниях нагрузки трансформатора его вторичное напряжение Измерение вторичного напряжения трансформатора при увеличении нагрузки от х.х. до номинальной является важнейшей характеристикой трансформатора и определяется выражением
Рис. 1.37. К выводу формулы Для определения
Измерение вторичного напряжения (1.67) с учетом (1.68) примет вид
Обозначим (Uk.a./U1ном)100=Uk.a.; (Uk.p./U1ном)100=Uk.p., тогда выражение изменения вторичного напряжения трансформатора при увеличении нагрузки примет вид
Выражение (1.70) дает возможность определить изменение вторичного напряжения лишь при номинальной нагрузке трансформатора. При необходимости расчета измерение вторичного напряжения для любой нагрузки в выражение (1.70) следует ввести коэффициент нагрузки, представляющий собой относительное значение тока нагрузки b=I2/I2ном
из выражения (1.71) следует, что изменение вторичного напряжения
Рис. 1.38. Зависимость
На рис. 1.38, а представлен график зависимости
Из (1.72) следует, что наибольшее значение изменения напряжения Зависимость вторичного напряжения
Рис. 1.39. Внешние характеристики трансфоматора. Вид внешней характеристики (рис. 1.39) зависит от характера нагрузки трансформатора (cosj2). Внешнюю характеристику трансформатора можно построить по (1.72) путем расчета Пример 1.6. Для трансформатора, данные которого приведены в примерах 1.4 и 1.5, (см. § 1.11.), определить изменение вторичного напряжения при номинальной нагрузке (b=1) с коэффициентом мощности cosj2 = 1,8 для нагрузок двух характеров: активно-индуктивной и ативно-емкостной. Решение. Из примера 1.4 имеем: uk75 =5,4%; cosφk75=0,4; sinφk75 =0,92. По (1.72) при cosφ2 = 0,8 и sinφ2 = 0,6 получим: для активно-индуктивной нагрузки ∆U=5,4(0,4•0,8+0,92•0,6)=4,65%; для активно-емкостной нагрузки ∆U = 5,4[0,4•0,8+0,92•(-0,6)]=-1,2%. В результате аналогичных расчетов, проделанных при β=0÷1,2, для нагрузок с cosφ2, равным 0,7; 0,8; 0,9 и 1,0, получены данные, по которым построены графики ∆U = f(β), представленные на рис 1 38, а. Наибольшее изменение напряжения соответствует активно-индуктивной нагрузке с cosφ2 = cosφk75 = 0,40 и коэффициенту нагрузки β = 1 (перегрузка трансформатора недопустима) ∆U тax = uk75= 5,4% (см рис. 1.38, 6)
|

 меняется. В этом можно убедится, воспользовавшись упрощенной схемой замещения трансформатора (см. рис. 1.35.), из которой следует, что
меняется. В этом можно убедится, воспользовавшись упрощенной схемой замещения трансформатора (см. рис. 1.35.), из которой следует, что 
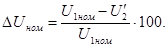 (1.67)
(1.67)

 , получим точку D. С некоторым допущением будем считать, что отрезок
, получим точку D. С некоторым допущением будем считать, что отрезок  представляет собой разность
представляет собой разность  , где
, где 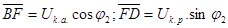 , тогда
, тогда (1.68.)
(1.68.) (1.69)
(1.69) (1.70)
(1.70) (1.71)
(1.71) зависит не только от величины нагрузки трансформатора (b), но и от характера этой нагрузки (j2).
зависит не только от величины нагрузки трансформатора (b), но и от характера этой нагрузки (j2).
 при cosj2=const, а на рис. 1.38, б – график
при cosj2=const, а на рис. 1.38, б – график  при b=const. На этих графиках отрицательные значения
при b=const. На этих графиках отрицательные значения  получим еще одно выражение для расчета изменения вторичного напряжения при любой нагрузке:
получим еще одно выражение для расчета изменения вторичного напряжения при любой нагрузке: (1.72)
(1.72) имеет место при равенстве углов фазового сдвига j2=jк, тогда cos(jk-j2)=1.
имеет место при равенстве углов фазового сдвига j2=jк, тогда cos(jk-j2)=1. трансформатора от нагрузки
трансформатора от нагрузки  называют внешней характеристикой. Напомним, что в силовых трансформаторах за номинальное напряжение на зажимах вторичной обмотки в режиме х.х. при номинальном первичном напряжении (см. § 1.3.).
называют внешней характеристикой. Напомним, что в силовых трансформаторах за номинальное напряжение на зажимах вторичной обмотки в режиме х.х. при номинальном первичном напряжении (см. § 1.3.).



