Розв’язання.
При n=1. У відповідності із формулою (1) в залежності від початкової суми с одержуємо з врахуванням табл.1. значення
Табл.2.
Припустимо далі, що кошти укладаються в два підприємства. Тоді у відповідності з формулою (4):
Отже, потрібно знайти значення функції (5) для всіх допустимих комбінацій с і х. Для зручності записи будемо оформляти у вигляді таблиць.
Табл.3.
Для кожного значення (20,40,60,80,100) початкової суми с розподіляючи коштів в табл.3. передбачений окремий рядок, а для кожного можливого значення х (0,20,40,60,80,100) – стовпець. Деякі клітинки таблиці залишаються незаповненими, тому що відповідають недопустимим комбінаціям с і х. Такою, наприклад, буде клітинка, яка відповідає рядку с = 40 і стовпцю х = 80, тому що при наявності 40 тис. грн. природно відпадає варіант, при якому одному із підприємств виділяється 80 тис. грн. В кожну клітинку таблиці будемо вписувати значення суми 80 – 60 = 20 тис. грн. При такому розподілі початкової суми на другому підприємстві буде забезпечений приріст продукції на суму в 36 тис. грн. (табл.1.), на першому – 10 тис. грн. (табл.2.). загальний прибуток складе (36+10) тис. грн., що і записано у відповідній клітинці табл.3. У двох останніх стовпцях таблиці проставлений по рядку приріст продукції (в стовпцях Розрахунок значень
Табл.4.
Перший додаток в табл.4. взяли із табл.1., другий із табл.3. Аналогічно знайдемо значення
Табл.5.
Результати обчислень запишемо у зведену таблицю 6.
Табл.6.
Таблиця 6 містить багато цінної інформації і дозволяє розв’язати цілий ряд задач. Із таблиці 6 видно, що найбільший приріст випуску продукції, яку можуть дати 4 підприємства при розподілі між ними 100 тис. грн. (С=100) складає 85 тис.грн. (f4(100)=85). При цьому четвертому підприємству необхідно виділити 40 тис. грн. 60 - 40 = 20 тис. грн. ЦІ 20 тис. грн. при оптимальному розподілі між двома підприємствами дадуть приріст продукції на суму 12 тис. грн.(f2(20)=12), при цьому другому підприємству потрібно асигнувати 20 тис. грн. Отже, максимальний приріст випуску продукції на чотирьох підприємствах при розподілі між ними 100 тис. грн. складає 85 тис. грн. і буде одержаний якщо першому підприємству коштів не виділяти, другому виділити 20 тис. грн., а третьому і четвертому – по 40 тис. грн.
Припустимо, що 100 тис. грн. потрібно розділити оптимально між трьома підприємствами. Із табл.6. знаходимо f3(100) = 79 тис.грн., приріст продукції на таку суму може бути одержаний при І нарешті, пропонується переконатись в оптимальності наступного розподілу 80 тис. грн. між двома підприємствами:
|

 , поміщенні в табл.2.
, поміщенні в табл.2.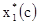

 x
c
x
c


 . Перший доданок беремо із умови задачі (табл.1.), другий із табл.2. Так, наприклад, при розподілі початкової суми с = 80 тис. грн. одним із варіантів може бути наступний: другому підприємстві виділяється 60 тис. грн. (х = 60), тоді першому
. Перший доданок беремо із умови задачі (табл.1.), другий із табл.2. Так, наприклад, при розподілі початкової суми с = 80 тис. грн. одним із варіантів може бути наступний: другому підприємстві виділяється 60 тис. грн. (х = 60), тоді першому ). Так, при початковій сумі с = 60 тис. грн. максимальний приріст продукції складає 43 тис. грн. (12+31), а це досягається виділенням другому підприємству 20, а першому – 60-20 = 40тис. грн.
). Так, при початковій сумі с = 60 тис. грн. максимальний приріст продукції складає 43 тис. грн. (12+31), а це досягається виділенням другому підприємству 20, а першому – 60-20 = 40тис. грн. наведений в табл.4. В даному випадку використана формула (4) при n=3:
наведений в табл.4. В даному випадку використана формула (4) при n=3:
 x
c
x
c

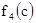 при n=4.
при n=4.
 x
c
x
c




 , а іншим трьом 100 –40 =60 тис. грн. Із цієї ж таблиці видно далі, що оптимальний розподіл цих 60 тис. грн. (С=60) між трьома підприємствами забезпечує загальний приріст продукції на суму 48 тис. грн. (f3(60)=48) при умові, що третьому підприємстві буде виділено 40 тис. грн.
, а іншим трьом 100 –40 =60 тис. грн. Із цієї ж таблиці видно далі, що оптимальний розподіл цих 60 тис. грн. (С=60) між трьома підприємствами забезпечує загальний приріст продукції на суму 48 тис. грн. (f3(60)=48) при умові, що третьому підприємстві буде виділено 40 тис. грн.  , а іншим двом:
, а іншим двом: , а на долю першого підприємства коштів не залишається (20 – 20 = 0).
, а на долю першого підприємства коштів не залишається (20 – 20 = 0).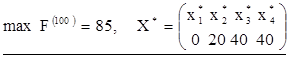
 , тобто якщо третьому підприємству асигнувати 40 тис. грн., а двом іншим 100 – 40 = 60 тис. грн. Ці кошти при оптимальному їх розподілі між двома підприємствами забезпечать приріст випуску продукції на суму f2(60) = 43 тис. грн. Але це можливо лише у тому випадку, якщо
, тобто якщо третьому підприємству асигнувати 40 тис. грн., а двом іншим 100 – 40 = 60 тис. грн. Ці кошти при оптимальному їх розподілі між двома підприємствами забезпечать приріст випуску продукції на суму f2(60) = 43 тис. грн. Але це можливо лише у тому випадку, якщо 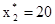 , тобто якщо другому підприємству виділити 20 тис. грн. Далі із таблиці 6 видно, що 60 – 20 = 40 тис. грн. слід асигнувати першому підприємству, тому що f1(40) = 31 при
, тобто якщо другому підприємству виділити 20 тис. грн. Далі із таблиці 6 видно, що 60 – 20 = 40 тис. грн. слід асигнувати першому підприємству, тому що f1(40) = 31 при  .
.



