Корреляционный и регрессионный анализ
Для оценки степени связи двух характеристик в корреляционном анализе используется коэффициент корреляции. Оценка коэффициента корреляции по наблюдениям
где
Значимость оценки определяется с помощью критерия Стьюдента: если
то оценка значима, и не значима в противном случае. Величина Для оценки характера связи в регрессионном анализе используется понятие функции регрессии. Оценка функции регрессии в нормальном случае производится по n наблюдениям
где
Доверительная область для линии регрессии r(х) определяется как:
где
Кa определяется по уровню значимости a(для В многомерном случае степень связи случайных величин Его оценка по n наблюдениям
где
Оценка множественной регрессии в виде линейной функции
Значимость оценок коэффициентов определяется из условий: • • • Оценка коэффициента является значимой, если значение соответствующей статистики превосходит табличное значение, отвечающее заданному уровню значимости.
|
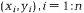рассчитывается по формуле:
выбирается из таблицы распределения Стьюдента [6] и отвечает уровню значимости а. (Для 
).
по формуле
).
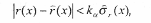
, Y определяется с помощью множественного коэффициента корреляции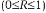 
определяется как:
– оценка функции множественной регрессии Y пo 
находится методом наименьших квадратов:
имеет распределение Стьюдента 
имеет распределение Стьюдента 
имеет распределение 
