Имитация функционирования систем с дискретными событиями
Класс систем управления, формализуемых в виде систем с дискретными событиями, достаточно широк и включает в себя большие информационно-управляющие системы, вычислительные системы, системы связи и др. При решении задачи программной имитации любой системы, в том числе и системы с дискретными событиями, составляется содержательное описание процесса функционирования, формализованное в виде математической модели. При этом определяются параметры модели, аппроксимирующие таблицы частот экспериментальных данных. При имитации функционирования систем на ЭВМ построенная математическая модель преобразуется в моделирующий алгоритм, в котором сохраняются логическая структура, последовательность протекания процесса во времени, характер и состав информации о состояниях процесса. ЭВМ представляют собой устройства дискретного типа, а потому и моделирующий алгоритм должен являться дискретной аппроксимацией построенной математической модели функционирования системы. Прямой путь решения данной задачи весьма прост. Интервал времени [0; Т], в течение которого рассматривается работа системы, разбивается на интервалы длиной ∆ t, из-за чего данный способ решения получил название принципа ∆ t. В пределах каждого интервала последовательно вычисляются приращения всех процессов в модели и производится, если это нужно, изменение состояния отдельных элементов модели. При достаточно малых ∆ t получаем хорошее приближение имитируемых процессов к процессам в реальной системе с параллельным выполнением операций. При таком способе построения моделирующего алгоритма точность моделирования достигается ценой больших затрат машинного времени. Обычно такой способ построения имитационных моделей используется при моделировании непрерывных динамических систем. Принцип ∆ t является наиболее универсальным принципом построения моделирующих алгоритмов, хотя и наименее экономичным с точки зрения вычислений на ЭВМ. Однако данный способ мало пригоден для решения задач имитации больших информационных систем, динамика которых состоит в переходе из состояния в состояние, причем в промежутках между переходами состояние системы остается неизменным. Каждый такой переход связан с наступлением некоторого события в системе, например приход входного либо управляющего дискретного сигнала, приход требования, отказ элемента, достижение некоторой характеристикой системы заданного порогового значения и др. Анализ различных алгоритмов моделирования для такого класса систем, проведенный в [2], показал, что наиболее часто используется принцип особых состояний. При построении алгоритма имитации функционирование системы, формализованное в математической модели, рассматривается как совокупность параллельно протекающих процессов, причем каждый процесс есть некоторая последовательность событий. С каждым событием связано изменение состояния системы. Событие, возникающее в системе, определяется как особое состояние. Процессы в общем случае не являются независимыми, а взаимодействуют между собой. Для иллюстрации данных понятий рассмотрим пример. Пример. Пусть в систему массового обслуживания, состоящую из одного прибора для обслуживания, поступает поток требований. Если требование, придя в систему, застает прибор свободным, то оно занимает прибор и обслуживается в нем в течение некоторого времени, после чего покидает систему. В противном случае требование поступает в очередь к прибору, где будет дожидаться конца обслуживания всех ранее поступивших в систему требований. В такой системе возможны 2 процесса: 1) процесс поступления требований; 2) процесс «захвата» прибора и обслуживания требований, причем процесс поступления требований инициирует второй процесс, если последний был приостановлен по причине отсутствия требований. Под состоянием системы будем понимать число требований, находящихся в системе. Из алгоритма функционирования видно, что состояние системы изменяется либо под влиянием событий процесса №1 (приход требований), либо под влиянием событий процесса №2 (захват и обслуживание). Анализ содержания данного примера показывает, что для развертывания совокупности параллельно протекающих процессов в последовательный необходимо упорядочить во времени моменты наступления событий каждого из процессов. Далее, сканируя по временной упорядоченной последовательности и имитируя в каждый наступивший момент особого состояния все необходимые действия, заданные в содержательном описании процесса функционирования системы как реакции системы на событие, получим имитационную модель алгоритма функционирования системы для ЭВМ. С целью формализации принципа особых состояний определим для каждого выделенного процесса момент
где r – номер процесса, в котором наступило ближайшее событие. Моменты системного времени, в отличие от реального времени, в котором работает моделирующая ЭВМ.
Рассмотрим структурную схему моделирующего алгоритма (рис. 9.1, стр. 198) и назначение основных операторов. Оператор задания начальных условий А содержит: · оператор задания начальных условий для моделируемого варианта А1, · оператор задания начальных условий для одной реализации (одного имитационного эксперимента) А2. Оператор определения очередного момента изменения состояния системы В находит момент наступления наиболее раннего события в соответствии с формулой (9.1) и определяет вид состояния системы, в которое она переходит в данный момент времени. Таким образом, оператор В содержит два массива: массив времени Ti, и массив состояний Логический оператор С осуществляет переход по номеру наступившего события к соответствующему оператору Di, имитирующему реакцию системы на событие. Оператор реакции Di имеет следующие основные функции:
Рис. 9.1. Структурная схема моделирующего алгоритма поведения системы управления · выполняет все необходимые операции, предусмотренные в алгоритме функционирования системы, как реакцию на данное событие; · вычисляет и накапливает интересующую системотехника статистику по исследуемым характеристикам системы, если она относится к данному процессу; · определяет момент следующего наступления события в данном процессе, состояние системы и заносит их в соответствующие массивы для оператора В; · вычисляет и заносит в массивы оператора В моменты наступления событий и состояние в других процессах, если последние были приостановлены, а инициирование их возможно только событием данного процесса. Следует заметить, что если процесс переходит в приостановленное состояние, то время наступления очередного события определить нельзя. В этом случае обычно принимают Оператор реакции
|

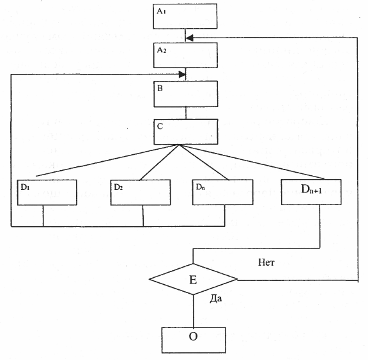
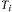 наступления очередного события i -го процесса и, если таких процессов будет n, то выбор наиболее раннего момента наступления особого состояния определится в соответствии с операцией:
наступления очередного события i -го процесса и, если таких процессов будет n, то выбор наиболее раннего момента наступления особого состояния определится в соответствии с операцией:
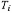 называются моментами
называются моментами
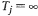 (где j – номер такого процесса) для того, чтобы исключить этот процесс из массива T в силу соотношения (9.1). Данный процесс активизируется только в случае инициирования его событиями других процессов.
(где j – номер такого процесса) для того, чтобы исключить этот процесс из массива T в силу соотношения (9.1). Данный процесс активизируется только в случае инициирования его событиями других процессов. обычно вводится в тех случаях, когда имитация производится на ограниченном интервале длины
обычно вводится в тех случаях, когда имитация производится на ограниченном интервале длины  – длительность одного имитационного эксперимента. Когда T0 окажется очередным моментом изменения состояния, тогда управление передается блоку
– длительность одного имитационного эксперимента. Когда T0 окажется очередным моментом изменения состояния, тогда управление передается блоку 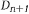 , выполняющему все необходимые действия по завершению одного имитационного эксперимента. Если не проведено достаточное для статистической точности число экспериментов, что проверяется оператором Е, то осуществляется возврат к оператору А2, в противном случае проводится обработка результатов в блоке оператора О (окончание) и выдача результатов имитационных экспериментов на устройство печати.
, выполняющему все необходимые действия по завершению одного имитационного эксперимента. Если не проведено достаточное для статистической точности число экспериментов, что проверяется оператором Е, то осуществляется возврат к оператору А2, в противном случае проводится обработка результатов в блоке оператора О (окончание) и выдача результатов имитационных экспериментов на устройство печати.


