Решение задачи ЛП с любым видом ограничений.Метод искусственного базиса. М-метод). Если система ограничений представлена неравенствами вида Пример:
Приведем задачу к каноническому виду:
Данная система не решена относительно положительного единичного базиса, введем в нее искусственные переменные х7 и х8, не имеющих никакого отношения к содержательной постановке задачи, но позволяющие получить начальный допустимый базис. Для исключения из базиса этих переменных, их вводят в целевую функцию с большим отрицательным коэффициентами М. Таким образом из исходной получается новая М – задача.
Выбрав в качестве начального базиса векторы А5,А7,А8, решаем полученную М – задачу с помощью табличного симплекс-метода. Для этого рассчитаем оценки (строку Выразим х7 и х8 из ограничений:
Подставим эти выражения в целевую функцию и приведем подобные:
Заполним первую симплекс таблицу:
Дальнейший расчет как в предыдущем методе. Постепенно из решения задачи уйдут все искусственные переменные.
|
или равенствами, то начальный опорный план не может быть найден так же просто, как в предыдущем методе. В таких случаях начальный опорный план отыскивается с помощью искусственных переменных.
).
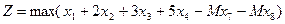
