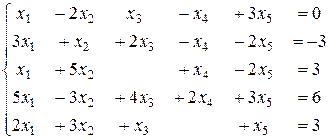Заметим, что систему ступенчатого вида всегда можно привести к виду (4) перестановкой столбцов и переобозначением номеров неизвестных.
Если свободным неизвестным присвоить произвольные значения, то из полученной системы можно определить значения базисных неизвестных. В этом случае система имеет бесконечное множество решений, то есть совместна и неопределённа. Если все свободные неизвестные положить равными нулю, то полученное таким образом решение будем называть базисным решением системы. Очевидно, что базисным решением однородной системы будет нулевое решение. Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением. Если свободные неизвестные выражены через параметры, а базисные неизвестные выражены через свободные неизвестные, то есть через те же параметры, то получается решение, которое называется общим решением. Если в приведённой системе (4) все неизвестные базисные, и она не содержит уравнения вида (3), то исходная система имеет единственное решение, то есть является определенной. Определённая система с п переменными приводится к ступенчатому виду так, что все коэффициенты aii = 1, i = 1,2,¼, n. Такой ступенчатый вид системы называется диагональным. Если в однородной системе число неизвестных превосходит число уравнений, то такая система неопределённа. Это следует из того, что если матрицу такой системы привести к ступенчатому виду, то в системе уравнений с полученной ступенчатой матрицей, во-первых, не может быть уравнений типа (3), и, во-вторых, не может не быть свободных неизвестных. В системах уравнений 1. и 2. найти общее решение, найти базисное решение. 1. 2. Решить системы уравнений. 3. 5. Ответы. 1.Возможный вариант базисного решения: 2..Возможный вариант базисного решения:
3.Система несовместна 4. Возможный вариант базисного решения: 5. Система несовместна
|



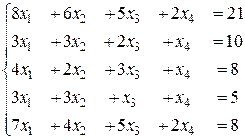 4.
4.