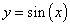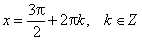- Перейдіть на лист2 у програмі Excel.
- Створіть таблицю «Зріст групи», структуру якої показано на рис. Заповніть стовпчики А і В даними (має бути не менш ніж 20).
- Виконайте обчислення: середнього зросту хлопців; середнього зросту дівчат, визначити зріст: найвищого хлопця; найвищої дівчини; найнижчого хлопця, найнижчої дівчини.
- Визначити стандартне відхилення даних від середнього.
- Зробити висновки.
- Збережіть дані та закрийте файл.
Контрольні запитання.
- Для чого призначені арифметичні функції?
- Для чого призначені тригонометричні функції?
- Які функції для виконання операцій ділення ви знаєте? Поясніть особливості аргументів таких функцій?
- Якою функцією слід скористатися для обчислення кореня квадратного з числа? Поясніть, яким має бути число, щоб у результаті роботи формули не було повідомлення про помилку.
- Чи можна застосовувати функцію СТЕПЕНЬ для обчислення кореня квадратного з числа?
- Коли доречно застосовувати функцію СУММЕСЛИ?
- Наведіть приклади застосування функції ПРОИЗВЕД.
8. Поясніть особливості застосування тригонометричних функцій.
- Для чого потрібні статистичні функції?
- Чим відрізняється робота функції НАИБОЛЬШИЙ / функції МАКС?
- Для чого призначена функція СРЗНАЧ?
- Якими мають бути аргументи статистичних функцій СТАНДОТКЛОН?
- Поясніть відмінність у роботі функції СРЗНАЧ під час обробки даних з діапазону комірок А (де є порожні комірки) та з діапазону комірок В (де замість порожніх комірок є комірки з нулевими значеннями).
- Для чого призначена функція СТАНДОТКЛОН? Продемонструйте роботу функції на прикладі.
Лабораторная работа №6
Тема
Построение тригонометрических функций.
Задание
Написать программу, которая строит любые тригонометрические функции и дает пользователю возможность выбора функции с дальнейшей ее визуализацией на экране монитора.
Теоретические сведения
Функция синус
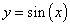

|
Область определения функции— множество Rвсех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2 π;:
sin(x+2 π· k) = sin x, где k ∈ Z для всех х ∈ R.
sin x = 0 при x = π·k, k ∈ Z.
sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z.
sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
| Функция возрастает от −1 до 1 на промежутках:
| 
| | Функция убывает от −1 до 1 на промежутках:
| 
| | Наибольшее значение функции sin x = 1в точках:
| 
| | Наименьшее значение функции sin x = −1в точках:
| 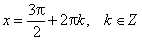
| |