Найпростіші схеми правильних міркувань
1. Правило заключення (А де А Þ В – загальна умова, А (а) – конкретна умова, В (а) – висновок (заключення). 2. Правило заперечення (А Þ В, В (а)) Þ 3. Правило силлогізму (підсилювання). (А Þ В, В Þ С) Þ (А Þ С)
У математиці існує ряд загальних методів доведення теорем. Розглянемо деякі з них. Дедуктивне доведення. Це основний метод математичних доведень. Кожен його крок ґрунтується на певному логічному законі, аксіомі або даних теорем, і все доведення є ланцюжок логічних умовиводів. При такому доведенні з правильних умов теореми ми з необхідністю дістаємо правильний висновок. Наприклад, теорема: «Якщо число ділиться на 2 і на 3, то, оскільки воно ділиться на 2 і не ділиться на 6, воно не ділиться на 3». Введемо позначення: А- «число ділиться на 2», В – «число ділиться на 3», С – «число ділиться на 6». Доведення цієї теореми запишемо за допомогою послідовних дедуктивних умовиводів. 1) А, В – умова теореми; 2) А 3) А 4) (А 5) (А На третьому кроці використано теорему: якщо число ділиться на кожне з двох взаємно простих чисел, то воно ділиться і на їхній добуток. Повна індукція. Термін «індукція» походить від латинського induktio – наведення. У математиці використовуються повна й неповна індукції. Доведення методом повної індукції полягає в розгляді всіх окремих випадків (чисел, фігур тощо), при яких теорема правильна. Кількість таких випадків повинна бути скінченною і невеликою за кількістю. Теорема: Значення виразу с = а2 + b 2, (а, b Доведення теореми проведемо, розглядаючи три випадки: 1) обидва числа парні; 2) обидва числа непарні; 3) одне число парне, друге – непарне. Нехай а, b – парні, тобто а = 2 m, b = 2 n, m, n с = (2 m)2 + (2 n)2 = 4 m 2 + 4 n 2 = 4∙ (m 2 + n 2), тобто с Нехай а, b – непарні числа, тобто а = 2 m + 1, b = 2 n + 1, m, n с = (2 m + 1)2 + (2 n + 1)2 = 4 m 2 + 4 m + 1 + 4 n 2 + 4n + 1= 4 (m 2 + n 2 + m + n) + 2, а це означає, що при ділені с на 4 дістанемо остачу 2, а не 3. Випадок 3) спробуйте розглянути самостійно.
|

 В, А (а)) Þ В (а),
В, А (а)) Þ В (а),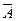 (а)
(а) В;
В; С;
С;
 );
);
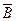 ).
).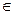 Z) є число, що при діленні на 4 не має остачі 3.
Z) є число, що при діленні на 4 не має остачі 3. 4, остача 0.
4, остача 0.


