Види теоремНехай дана теорема АÞВ. Теореми АÞВ, ВÞА називаються зворотними один одному. А теореми А Þ В та Теорему Наприклад, дана теорема «Якщо кути вертикальні, то вони рівні». Сформулюємо теорему зворотну, протилежну та зворотно протилежну. Зворотна даній: Якщо кути рівні, то вони вертикальні. – Це хибне висловлення. Протилежне даної: Якщо кути не є вертикальними, то вони не рівні. – Це хибне висловлення. Зворотньо протилежна: Якщо кути не рівні, то вони не вертикальні. – Це істинне висловлення. Чи існує зв’язок між названими видами теорем? З’ясовано, що теореми А Þ В та
Отриману рівність називають законом контропозиції.
Після того, як доведена яка-небудь теорема виду АÞВ, має сенс досліджувати зворотну їй теорему. У кожному випаду потрібно проводить її самостійний доказ, тому що теорема, зворотна даної, може бути помилковою. Так трапилося, наприклад, у розглянутому вище прикладі. Якщо виявляться вірними і дана теорема і їй зворотна, то можна їх об'єднати в одну за допомогою слів «тоді і тільки тоді, коли» або «необхідно і достатньо».
|
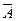Þ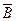 
називаються протилежними один одному.
