Лабораторна робота № 8. Тема: Програми циклічної структури
Тема: Програми циклічної структури. Оператор циклу з параметром. Мета:Формування вмінь і навичок програмування алгоритмів циклічної структури для перебору рівномірно розподілених значень. Формування вмінь і навичок програмування алгоритмів з використання вкладених циклів. Закріплення вмінь і навичок використання вказівок вводу-виводу. Застосування вмінь і навичок програмування алгоритмів лінійної та розгалуженої структури. Контрольні запитання: 1. Який вигляд має цикл з параметром? 2. Який порядок виконання оператора циклу з параметром? 3. Чи можна здійснити достроковий вихід із циклу з параметром? Чи коректно це робити? 4. Які значення може приймати величина кроку в циклі з параметром? 5. Розпишіть покроково виконання двох наступних фрагметнів програми:
6. Чи виконуватиметься цикл з параметром, якщо при додатньому значенні кроку початкове значення параметра циклу перевищує кінцеве значення? 7. Які значення може приймати параметр перелічувального циклу? 8. До якого типу змінних має належати параметр перелічувального циклу? 9. Чи виконуватиметься перелічувальний цикл при відсутності параметра? 10. Чи можна змінювати значення параметру в тілі циклу? 11. Елементи яких структур може послідовно перебирати перелічувальний цикл? Чи виконуватиметься перелічувальний цикл при відсутності такої структури? 12. Які цикли називають вкладеними? 13. Скільки разів виконується тіло вкладеного циклу? 14. Поясніть дію груп операторів: FOR I=1 TO 5 DO FOR J=2 TO 4 DO A:=I+J; 14. Поясніть дію груп операторів: FOR I=1 TO 5 DO BEGIN FOR J=2 TO 4 DO A:=I+J; FOR K=1 TO 7 DO B:=I+K; END;
Завдання 1. Скласти програму обчислення значень функції F(X) на відрізку [A,B] в точках Xi=A+iH, де H=(B-A)/M, M – задане ціле число. Вимоги до програми: - для задання значень Х і відповідних значень функції потрібно використовувати прості змінні; - значення кроку Н повинно обчислюватись один раз; - при зміні значення аргумента Х використовувати оператор присвоєння Х:=Х+Н, а не оператор з використанням операції множення Х:=А+І*Н (що істотно скорочує час виконання програми); - значення аргументів та відповідні їм значення результатів вивести на екран у вигляді таблиці.
Завдання 2. Ввести послідовність нулів і одиниць, які є записами числа в двійковій системі числення. Кількість символів (N), що потрібно ввести, вказана в таблиці. Перевести число в десяткову систему числення і визначити, чи кратне воно М. Вивести на екран число в двійковій і десятковій системах числення і відповідь щодо кратності його числу М.
Завдання 3. Скласти програму для розв'язання поставленого завдання. Вимоги до програми: – числові значення параметрів обчислень ввести з клавіатури з відповідною перевіркою коректності даних та їх типів; – при створенні програми використати вкладені цикли; – результати обчислень вивести на екран в одному діалоговому вікні.
Варіанти:
1. Знайти натуральне число в межах від 1 до 10000 з максимальною сумою дільників. 2. Дано натуральне число N. Отримати всі менші за N натуральні числа, що є з ним взаємно прості. 3. Дано цілі числа Р та Q. Отримати всі дільники числа Q, взаємно прості з Р. 4. Дано натуральне число N. Отримати всі прості дільники цього числа. 5. Знайти найменше натуральне число N, яке можна подати двома різними способами у вигляді N=х3+y3 (x>у). 6. Дано натуральні числа А та В (А<В). Отримати всі прості числа Р з проміжку [A;B]. 7. Знайти сто перших простих чисел. 8. Дано натуральні числа N та М. Отримати всі менші N натуральні числа, квадрат суми цифр яких рівний М. 9. Дано натуральне число N. Отримати всі менші за N досконалі числа. (Натуральне число називається досконалим, якщо воно рівне сумі всіх своїх дільників, за винятком самого себе. Наприклад, число 6 – досконале, оскільки 6=1+2+3, а число 8 – недосконале, оскільки 8 10. Дано натуральне число N. З¢ясувати, чи можна подати його у вигляді суми квадратів трьох натуральних чисел. Якщо можна, то вказати таку трійку х, у, z натуральних чисел, що N=x2+y2+z2. 11. В інтервалі від 1 до 1000 знайти всі пари простих чисел. (Парою простих чисел називаюся два простих числа, різниця між якими рівна 2, наприклад: 3 і 5, 11 і І3, 17 і 19). 12. Відомо, що будь-яке натуральне число Р (Р>7) можна подати у вигляді Р=3А+5В. Знайти всі пари чисел А та В для числа Р. 13. Дане натуральне число Р (Р<100000). Отримати всі дружні числа в інтервалі від 1 до Р. (Дружніми числами називається така пара натуральних чисел М і N, для яких сума всіх дільників числа М (крім самого числа М) рівна N, а сума всіх дільників числа N (крім самого числа N) рівна M. Наприклад, числа 220 і 284 дружні, оскільки сума дільників числа 220 (1+2+4+5+10+11+20+22+44+55+110) рівна 284, а сума дільників числа 284 (1+2+4+71+142) рівна 220). 14. Число Армстронга – це таке число із K цифр, для якого сума К-х степенів його цифр рівна самому числу. Наприклад: 153=13+53+33. Знайти всі числа Армстронга з двох, трьох, чотирьох цифр. 15. Дано натуральне число N. З¢ясувати, чи можна подати його у вигляді суми кубів двох натуральних чисел. Якщо можна, то вказати два таких натуральних числа х та у, що N=х3+y3.
|









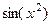


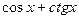



 1+2+4).
1+2+4).


