Теоретичні аспекти врахування фактору часу у фінансових операціях.
У фінансовому менеджменті врахування фактору часу здійснюється за допомогою нарощування і дисконтування, в основі яких враховується техніка процентних обчислень. За допомогою цих методів здійснюється приведення грошових сум, що відносяться до різних тимчасових періодів, до необхідного моменту часу в сьогоденні або майбутньому. При цьому в якості норми приведеня використовується процентна ставка (interest rate - r). У вузькому значенні процентна ставка являє собою ціну, що сплачується за використання позикових коштів. Під нарощенням розуміють процес збільшення первісної суми в результаті нарахування відсотків. Зміст метода нарощування полягає у визначені величини, яка буде або може бути одержана з деякої початкової (поточної) суми в результаті проведення операції. Іншими словами, метод нарощування дає можливість визначити майбутню величину (future value - FV) поточної суми (present value - PV) через деякий проміжок часу, виходячи з заданої процентної ставки r. Дисконтування являє собою процес знаходження величини на заданий момент часу по її відомому або передбачуваному значенню в майбутньому. В фінансових розрахунках величина PV, знайдена в процесі дисконтування, показує сучасне (з позиції сучасного моменту часу) значення майбутньої величини FV. Цілком очевидним є те, що дисконтування, по суті, є дзеркальним відображенням нарощення. Процентну ставку r, що використовується при цьому називають нормою дисконту. Методи нарощення й дисконтування відіграють важливу роль у фінансовому аналізі, тому що є інструментарієм для оцінки потоків платежів (cash flows). Для оволодіння даним питанням у практичній площині розглянемо наступну задачу. Сума в 10000 грн. поміщена в банк на депозит строком на 4 роки. Ставка по депозиту – 10% річних. Відсотки по депозиту нараховуються раз на рік. Яка буде величина депозиту в кінці терміну? За умовами даної задачі відомими величинами є: первинна сума внеску PV = 10000 у.о., процентна ставка r= 10% і термін n = 4 роки. Визначимо майбутню величину внеску FV на кінець першого періоду (року): FV1 = PV + PV*r = PV*(1+r) = 10000*(1+0,1) = 10000*1,1 = 11000. Відповідно для другого періоду величина FV буде рівна: FV2 = FV1 + FV1*r = PV*(1+r)+PV*(1+r)*r = PV*(1+r)2 = 10000*(1+0,1)2 = 12100. Для останнього періоду (n = 4): FV4 = FV3 + FV3 * r = PV*(1+r)4 = 10000*(1+ 0,1)4 = 14641. Виходячи з наведених даних майбутню величину внеску FV можна визначити використовуючи формулу 1.
Цілком очевидно, що величина FVістотно залежить від значень r і n. Наприклад, майбутня величина суми всього в 1,00 у.о. при річній ставці 15% через 100 років складе 1174313,45 у.о. В процесі кількісного аналізу фінансових операцій, зручно абстрагуватися від їх конкретного економічного змісту і розглядати породжувані ними рухи грошових коштів як чисельний ряд, що складається з послідовності розподілених в часі платежів CF0, CF1,..., CFn . Для позначення подібного ряду в світовій практиці широко використовується термін “ потік платежів” або “ потік грошей” (cash flow – CF). Окремий елемент такого чисельного ряду CFtє різницею між всіма надходженнями (притоками) грошових коштів і їх витрачанням (відтоками) на конкретному тимчасовому відрізку проведення фінансової операції. Таким чином, величина CFt може мати як позитивний, так і негативний знак. Кількісний аналіз грошових потоків, що генеруються за певний період часу в результаті реалізації фінансової операції, або функціонування яких-небудь активів, в загальному випадку зводиться до розрахунку наступних характеристик: FVn – майбутньої вартості потоку за n періодів; PVn – сучасної вартості потоку за n періодів. Часто виникає необхідність визначення і ряду інших параметрів фінансових операцій, найважливішими з яких є: CFt – величина потоку платежів в періоді t; r– процентна ставка; n – термін (кількість періодів) проведення операції. В цілому, розглянута теорія дає можливість стверджувати, що простий (елементарний) потік грошей складається з однієї виплати і подальшого надходження, або разового надходження з подальшою виплатою, розділених n - періодами часу (для прикладу – роками). Прикладами фінансових операцій з подібними потоками платежів є термінові депозити, одноразові позики, деякі види цінних паперів тощо. Неважко відмітити, що чисельний ряд в цьому випадку складається всього з двох елементів – {-PV; FV} або {PV; -FV}. На практиці, залежно від умов фінансової операції, відсотки можуть нараховуватися кілька разів в році, наприклад щомісячно, щокварталу і т.д. В цьому випадку співвідношення (1) для розрахунку майбутньої вартості матиме наступний вигляд:
де m – число періодів нарахування в році. Очевидно, що чим більше m, тим швидше йде нарощування суми. Допустимо, що в наведеному прикладі відсотки виплачуються щокварталу, тобто r = 4. В такому випадку величина майбутньої вартості FV = 10000,00*(1 + 0,10/4)16 = 14845,06 у.о., тобто на 204,06 більше, ніж при нарахуванні відсотків раз на рік. Часто виникає необхідність порівняння умов фінансових операцій, що передбачають різні періоди нарахування відсотків. В цьому випадку здійснюють приведення відповідних процентних ставок до їх річного еквівалента:
де r – номінальна ставка; m – число періодів нарахування. Одержану при цьому величину називають ефективною процентною ставкою (effective percentage rate – EPR) або ставкою порівняння. Ефективна процентна ставка для наведеного прикладу дорівнює 0,103813, тобто ЕPR = (1+0,1/4)4-1 = 0,103813. Майбутня величини внеску у цьому випадку становить FV = 10000*(1+0,103813)4 = 14845,06 у.о. Таким чином, умови розміщення суми в 10000 у.о. під депозит строком на 4 роки під 10% річних при щоквартальному нарахуванні відсотків і під 10,381%, разів на рік, що нараховуються, є еквівалентними. Формулу для визначення початкової (сучасної) величини елементарного потоку платежів можна легко вивести із співвідношення (1), шляхом ділення його обох частин на величину (1+r)n. Виконавши відповідні математичні перетворення, одержимо наступну формулу:
Визначити первинну величину внеску PV, якщо ставка по депозиту рівна 10% річних, а виплачена після 4-х річного депозиту сума склала величину в 14641 у.о. При даних умовах PV = 14641/(1+0,1)4 = 10000. Як показують розрахунки, величина PV залежить від тривалості операції і процентної ставки, проте залежність тут зворотна – чим більше r і n, тим менше поточна (сучасна) величина. У випадку, якщо нарахування відсотків здійснюється m-раз в році, співвідношення (1) матиме наступний вигляд:
Формули для визначення величин r і n можуть бути одержані з виразу (1) і мають наступний вид. При відомих величинах FV, PV і n, процентну ставку r можна визначити за формулою:
Визначити процентну ставку (прибутковість операції), якщо сума в 10000 у.о. поміщена в банк на 4 роки і склала величину в 14641 у.о. r = (14141/10000)*1/4 - 1 = 0,10 (10%). Величина n розраховується за формулою: Таким чином операції з елементарними потоками платежів характеризуються чотирма основними параметрами: FV, PV, r та n. При цьому величина будь-якого з них може бути визначена по відомих значеннях трьох інших, при цьому можуть бути використані загальні методи роботи з Excel, до яких відносяться фінансові функції, відповідні інструментарії – Подбор параметра, Таблицы подстановки, Сценарии.
|

 (1)
(1) (2)
(2) (3)
(3)
 (4)
(4) (5)
(5)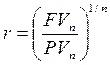 (6)
(6) , причому тривалість розрахунку залежить від швидкості реалізації логарифмування.
, причому тривалість розрахунку залежить від швидкості реалізації логарифмування.


