 Û
Û  .
.
Поскольку  То область допустимых значений для данного неравенства – объединение интервалов:
То область допустимых значений для данного неравенства – объединение интервалов:  . Следовательно, с учетом правила раскрытия модулей,
. Следовательно, с учетом правила раскрытия модулей,  при решении данного неравенства необходимо рассмотреть три случая:
при решении данного неравенства необходимо рассмотреть три случая:  ,
,  и
и  .
.
1) Пусть  , тогда
, тогда 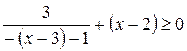 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Следовательно, решением неравенства на интервале
. Следовательно, решением неравенства на интервале  является множество
является множество  .
.
2) Пусть  , тогда
, тогда  ,
,  ,
,  ,
,  ,
, 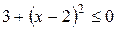 , чего быть не может. Следовательно, на интервале
, чего быть не может. Следовательно, на интервале  неравенство решений не имеет.
неравенство решений не имеет.
3) Пусть  , тогда
, тогда  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
Это означает, что если  , то
, то  ,
,  и неравенство на данном интервале решений не имеет; если
и неравенство на данном интервале решений не имеет; если  , то
, то  ,
,  и решением неравенства на этом интервале является множество
и решением неравенства на этом интервале является множество  .
.
Таким образом, решениями исходного неравенства являются  .
.
Ответ:  .
.
| Содержание критерия
| Баллы
|
| Обоснованно получен верный ответ
|
|
| Допущена единичная вычислительная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 18 В трапеции  основания
основания  и
и  относятся как
относятся как  . Пусть К – середина диагонали
. Пусть К – середина диагонали  . Прямая
. Прямая  пересекает прямую
пересекает прямую  в точке
в точке  .
.
а) Докажите, что 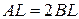 .
.
 б) Найдите площадь четырехугольника
б) Найдите площадь четырехугольника  , если известно, что площадь трапеции
, если известно, что площадь трапеции  равна 9.
равна 9.
Решение. Пусть ABCD указанная трапеция (смотрите рисунок 3).

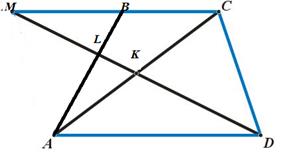
Рисунок 3 Рисунок 4
а) Сделаем дополнительное построение: продолжим отрезки ВС и DL до их пересечения и обозначим получившуюся точку – M (смотрите рисунок 4).
Треугольники АКD и МКС равны (по стороне и двум прилежащим углам:  ), следовательно,
), следовательно,  , что означает, что четырехугольник
, что означает, что четырехугольник  - параллелограмм (смотрите рисунок 5), а поскольку по условию
- параллелограмм (смотрите рисунок 5), а поскольку по условию  и
и  относятся как
относятся как  , то точка В – середина отрезка МС.
, то точка В – середина отрезка МС.

Рисунок 5
Треугольники  и
и 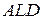 подобны по двум углам:
подобны по двум углам:  . Следовательно,
. Следовательно,  . Поскольку,
. Поскольку,  , получаем, что
, получаем, что  , т.е.
, т.е.  . Что и требовалось доказать.
. Что и требовалось доказать.
б) Пусть у трапеции ABCD длина основания ВС равна х, а длина высоты – h. Тогда, так как  , а согласно условию, и
, а согласно условию, и  , получаем уравнение:
, получаем уравнение:  , откуда следует, что
, откуда следует, что  .
.
 .
.
 , где 2 х – длина основания МС, а
, где 2 х – длина основания МС, а  - высота треугольника, опущенная из вершины К, являющейся серединой отрезка АС, и, следовательно,
- высота треугольника, опущенная из вершины К, являющейся серединой отрезка АС, и, следовательно,  и
и  .
.
 , где х – длина основания МB, а
, где х – длина основания МB, а  - высота треугольника, опущенная из вершины L. В силу того, что треугольники MBL и ALD являются подобными с коэффициентом подобия 2, то, их высоты, опущенные из вершины L, относятся, как 1:2, что означает, что
- высота треугольника, опущенная из вершины L. В силу того, что треугольники MBL и ALD являются подобными с коэффициентом подобия 2, то, их высоты, опущенные из вершины L, относятся, как 1:2, что означает, что  , и,
, и,  . Следовательно,
. Следовательно,  .
.
Ответ:  .
.
| Содержание критерия
| Баллы
|
| Имеется верное доказательство утверждения пункта а, и обоснованно получен верный ответ в пункте б
|
|
| Получен обоснованный ответ в пункте б,
ИЛИ
имеется верное доказательство утверждения пункта а, и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки
|
|
| Имеется верное доказательство утверждения пункта а,
ИЛИ
при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 19 1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т.е. увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платеж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные платы были не более 300 000 рублей?

 Û
Û  .
. То область допустимых значений для данного неравенства – объединение интервалов:
То область допустимых значений для данного неравенства – объединение интервалов:  . Следовательно, с учетом правила раскрытия модулей,
. Следовательно, с учетом правила раскрытия модулей,  при решении данного неравенства необходимо рассмотреть три случая:
при решении данного неравенства необходимо рассмотреть три случая:  ,
,  и
и  .
.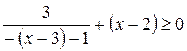 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Следовательно, решением неравенства на интервале
. Следовательно, решением неравенства на интервале  является множество
является множество  .
. ,
,  ,
,  ,
,  ,
, 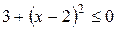 , чего быть не может. Следовательно, на интервале
, чего быть не может. Следовательно, на интервале  неравенство решений не имеет.
неравенство решений не имеет. ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  .
. , то
, то  ,
,  и неравенство на данном интервале решений не имеет; если
и неравенство на данном интервале решений не имеет; если  , то
, то  ,
,  и решением неравенства на этом интервале является множество
и решением неравенства на этом интервале является множество  .
. .
. основания
основания  и
и  относятся как
относятся как  . Пусть К – середина диагонали
. Пусть К – середина диагонали  . Прямая
. Прямая  пересекает прямую
пересекает прямую  в точке
в точке  .
.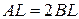 .
. , если известно, что площадь трапеции
, если известно, что площадь трапеции 

 ), следовательно,
), следовательно,  , что означает, что четырехугольник
, что означает, что четырехугольник  - параллелограмм (смотрите рисунок 5), а поскольку по условию
- параллелограмм (смотрите рисунок 5), а поскольку по условию 
 и
и 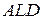 подобны по двум углам:
подобны по двум углам:  . Следовательно,
. Следовательно,  . Поскольку,
. Поскольку,  , получаем, что
, получаем, что  , т.е.
, т.е.  . Что и требовалось доказать.
. Что и требовалось доказать. , а согласно условию, и
, а согласно условию, и  , получаем уравнение:
, получаем уравнение:  , откуда следует, что
, откуда следует, что  .
. .
. , где 2 х – длина основания МС, а
, где 2 х – длина основания МС, а  - высота треугольника, опущенная из вершины К, являющейся серединой отрезка АС, и, следовательно,
- высота треугольника, опущенная из вершины К, являющейся серединой отрезка АС, и, следовательно,  и
и  .
. , где х – длина основания МB, а
, где х – длина основания МB, а  - высота треугольника, опущенная из вершины L. В силу того, что треугольники MBL и ALD являются подобными с коэффициентом подобия 2, то, их высоты, опущенные из вершины L, относятся, как 1:2, что означает, что
- высота треугольника, опущенная из вершины L. В силу того, что треугольники MBL и ALD являются подобными с коэффициентом подобия 2, то, их высоты, опущенные из вершины L, относятся, как 1:2, что означает, что  , и,
, и,  . Следовательно,
. Следовательно,  .
. .
. 


