1 й способ. Очевидно, что чем большую сумму он сможет возвращать, тем быстрее расплатится. Поскольку он взял 900 000, то с учетом процентов, начисленных банком, после первого платежа, величиной 300 000 рублей, его долг составит: 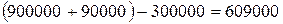 рублей. После второго платежа, величиной 300000 рублей, его долг составит:
рублей. После второго платежа, величиной 300000 рублей, его долг составит: 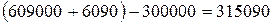 рублей. После третьего платежа величиной 300000 рублей его долг составит:
рублей. После третьего платежа величиной 300000 рублей его долг составит: 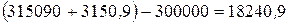 рублей. Величина последнего четвертого платежа в этом случае составит:
рублей. Величина последнего четвертого платежа в этом случае составит:  рублей. Таким образом, даже если он будет выплачивать максимально возможную для него сумму, то потребуется 4 месяца.
рублей. Таким образом, даже если он будет выплачивать максимально возможную для него сумму, то потребуется 4 месяца.
2 способ. Если бы банк не брал проценты, то долг можно было бы выплатить за 3 месяца, внося каждый раз 300 000 рублей. За три месяца банк заберет не более 3% от исходной суммы 900 000, т.е. переплата не может превысить 27 000 и их можно вернуть за четвертый месяц.
Ответ: 4 месяца.
| Содержание критерия
| Баллы
|
| Обоснованно получен верный ответ
|
|
| Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки
ИЛИ
получен верный ответ, но решение недостаточно обосновано
|
|
| Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение не завершено
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 20 Найдите все значения параметра а, при каждом из которых решения неравенства  образуют отрезок длины 1.
образуют отрезок длины 1.
Решение.  Û
Û  .
.
Рассмотрим функции 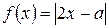 и
и 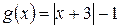 . Эскизы графиков данных функций представлены на рисунках 6 и 7 и соответственно.
. Эскизы графиков данных функций представлены на рисунках 6 и 7 и соответственно.
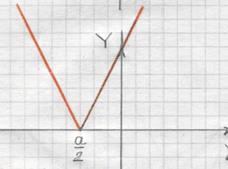
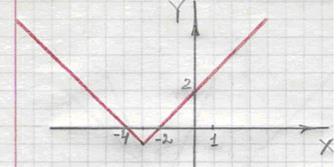
Рисунок 6 – График функции Рисунок 7 - График функции 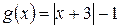
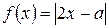
Поскольку 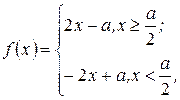 и соприкасается с осью ОХ только в точке с абсциссой
и соприкасается с осью ОХ только в точке с абсциссой 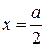 , а
, а 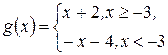 и пересекается с осью ОХ в двух точках с абсциссами - 2 и - 4 соответственно, то нетрудно заметить, что если
и пересекается с осью ОХ в двух точках с абсциссами - 2 и - 4 соответственно, то нетрудно заметить, что если 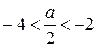 неравенство решений не имеет (смотрите рисунок 8).
неравенство решений не имеет (смотрите рисунок 8).
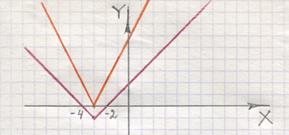
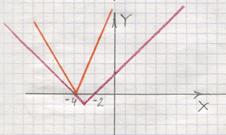
Рисунок 8 – 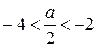 Рисунок 9 –
Рисунок 9 – 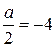
Если 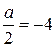 (смотрите рисунок 9), то решением является одно значение:
(смотрите рисунок 9), то решением является одно значение: 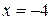 , если
, если 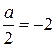 , то решением является одно значение:
, то решением является одно значение: 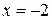 . Следовательно, нужно исследовать ситуации, когда
. Следовательно, нужно исследовать ситуации, когда 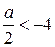 и когда
и когда 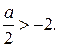
Пусть 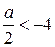 , т.е.
, т.е.  . Тогда графики функций пересекаются в двух точках (смотрите рисунок 10), решением неравенства будет отрезок
. Тогда графики функций пересекаются в двух точках (смотрите рисунок 10), решением неравенства будет отрезок 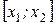 , где
, где 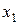 - решение уравнения
- решение уравнения  , а
, а 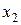 - решение уравнения
- решение уравнения 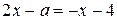 .
.

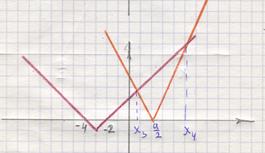
Рисунок 10 - 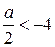 Рисунок 11 -
Рисунок 11 - 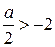 .
.
Следовательно,  . Длина отрезка в этом случае:
. Длина отрезка в этом случае:  и равна 1, если
и равна 1, если 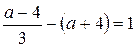 ,
, 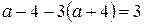 ,
,
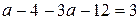 ,
, 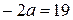 ,
, 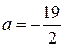 ,т.е.
,т.е.  .
.
Пусть 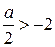 , т.е.
, т.е.  . Тогда графики функций также пересекаются в двух точках (смотрите рисунок 11), решением неравенства будет отрезок
. Тогда графики функций также пересекаются в двух точках (смотрите рисунок 11), решением неравенства будет отрезок  , где
, где  - решение уравнения
- решение уравнения 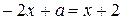 , а
, а 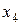 - решение уравнения
- решение уравнения  . Следовательно,
. Следовательно,  . Длина отрезка в этом случае:
. Длина отрезка в этом случае: 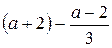 и равна 1, если
и равна 1, если 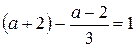 ,
, 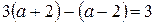 ,
, 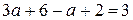 ,
, 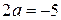 ,
, 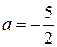 , т.е.
, т.е. 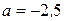 .
.
Ответ:при а = -2,5 и а = -9,5.
| Содержание критерия
| Баллы
|
| Обоснованно получен верный ответ
|
|
| С помощью верного рассуждения получены оба верных значения параметра, но
– или в ответ включены также одно-два неверных значения;
– или решение недостаточно обосновано
|
|
| С помощью верного рассуждения получено хотя бы одно верное значение параметра
|
|
| Задача сведена к исследованию взаимного расположения графиков функций, но не доведена до конца
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 21 Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 720 и
а) пять; б) четыре; в) три
из них образуют геометрическую прогрессию?

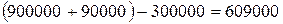 рублей. После второго платежа, величиной 300000 рублей, его долг составит:
рублей. После второго платежа, величиной 300000 рублей, его долг составит: 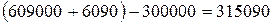 рублей. После третьего платежа величиной 300000 рублей его долг составит:
рублей. После третьего платежа величиной 300000 рублей его долг составит: 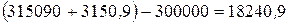 рублей. Величина последнего четвертого платежа в этом случае составит:
рублей. Величина последнего четвертого платежа в этом случае составит:  рублей. Таким образом, даже если он будет выплачивать максимально возможную для него сумму, то потребуется 4 месяца.
рублей. Таким образом, даже если он будет выплачивать максимально возможную для него сумму, то потребуется 4 месяца. образуют отрезок длины 1.
образуют отрезок длины 1. .
.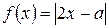 и
и 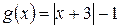 . Эскизы графиков данных функций представлены на рисунках 6 и 7 и соответственно.
. Эскизы графиков данных функций представлены на рисунках 6 и 7 и соответственно.

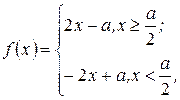 и соприкасается с осью ОХ только в точке с абсциссой
и соприкасается с осью ОХ только в точке с абсциссой 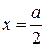 , а
, а 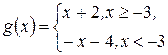 и пересекается с осью ОХ в двух точках с абсциссами - 2 и - 4 соответственно, то нетрудно заметить, что если
и пересекается с осью ОХ в двух точках с абсциссами - 2 и - 4 соответственно, то нетрудно заметить, что если 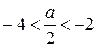 неравенство решений не имеет (смотрите рисунок 8).
неравенство решений не имеет (смотрите рисунок 8).

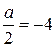
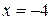 , если
, если 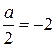 , то решением является одно значение:
, то решением является одно значение: 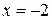 . Следовательно, нужно исследовать ситуации, когда
. Следовательно, нужно исследовать ситуации, когда 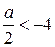 и когда
и когда 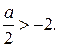
 . Тогда графики функций пересекаются в двух точках (смотрите рисунок 10), решением неравенства будет отрезок
. Тогда графики функций пересекаются в двух точках (смотрите рисунок 10), решением неравенства будет отрезок 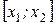 , где
, где 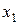 - решение уравнения
- решение уравнения  , а
, а 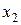 - решение уравнения
- решение уравнения 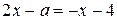 .
.

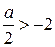 .
. . Длина отрезка в этом случае:
. Длина отрезка в этом случае:  и равна 1, если
и равна 1, если 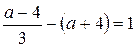 ,
, 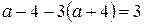 ,
,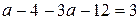 ,
, 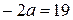 ,
, 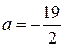 ,т.е.
,т.е.  .
. . Тогда графики функций также пересекаются в двух точках (смотрите рисунок 11), решением неравенства будет отрезок
. Тогда графики функций также пересекаются в двух точках (смотрите рисунок 11), решением неравенства будет отрезок  , где
, где  - решение уравнения
- решение уравнения 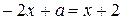 , а
, а 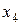 - решение уравнения
- решение уравнения  . Следовательно,
. Следовательно,  . Длина отрезка в этом случае:
. Длина отрезка в этом случае: 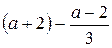 и равна 1, если
и равна 1, если 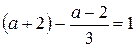 ,
, 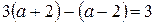 ,
, 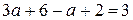 ,
, 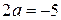 ,
, 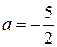 , т.е.
, т.е. 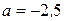 .
.


