 .
.
а) Предположим, что такие числа найдутся, тогда они могут быть представлены в виде:  , где
, где  (иначе числа не будут различными) и, следовательно,
(иначе числа не будут различными) и, следовательно,  ,
, 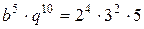 ,
,  Поскольку по условию b и q – натуральные числа и
Поскольку по условию b и q – натуральные числа и  , получившееся уравнение решений не имеет и предположение не является верным.
, получившееся уравнение решений не имеет и предположение не является верным.
б) Предположим, что такие числа найдутся, тогда четыре из них можно представить в виде:  , где
, где  (иначе числа не будут различными), а пятое принимает некоторое значение с. Тогда, согласно условию,
(иначе числа не будут различными), а пятое принимает некоторое значение с. Тогда, согласно условию,  ,
,  ,
,  . Поскольку по условию b, с, q – натуральные числа и
. Поскольку по условию b, с, q – натуральные числа и  , получившееся уравнение решений не имеет и предположение не является верным.
, получившееся уравнение решений не имеет и предположение не является верным.
в) Предположим, что такие числа найдутся, тогда три из них можно представить в виде:  , где
, где  (иначе числа не будут различными), а четвертое и пятое принимает некоторые значения с и d. Тогда, согласно условию,
(иначе числа не будут различными), а четвертое и пятое принимает некоторые значения с и d. Тогда, согласно условию,  ,
,  ,
,  . Поскольку по условию b, с, d, q – натуральные числа и
. Поскольку по условию b, с, d, q – натуральные числа и  , то выбирая
, то выбирая  получаем три числа, образующих геометрическую прогрессию: 1, 2, 4, произведение двух оставшихся чисел, отличных от уже найденных, должно быть равно 90. Следовательно, это могут быть числа: 3 и 30, 6 и 15, 9 и 10, 18 и 5.
получаем три числа, образующих геометрическую прогрессию: 1, 2, 4, произведение двух оставшихся чисел, отличных от уже найденных, должно быть равно 90. Следовательно, это могут быть числа: 3 и 30, 6 и 15, 9 и 10, 18 и 5.
Таким образом, число 720 в виде произведения пяти натуральных чисел, три из которых образуют геометрическую прогрессию может быть представлено следующим образом:
 ,
,  ,
,  ,
, 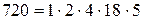 .
.
Ответ: а) нет; б) нет; в) да.
| Содержание критерия
| Баллы
|
| Верно получены все перечисленные (см. критерий на 1 балл) результаты
|
|
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов
|
|
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов
|
|
| Верно получен один из следующих результатов:
— обоснованное решение пункта а;
— обоснованное решение пункта б;
— искомая оценка в пункте в;
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|

 .
. , где
, где  (иначе числа не будут различными) и, следовательно,
(иначе числа не будут различными) и, следовательно,  ,
, 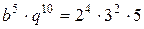 ,
,  Поскольку по условию b и q – натуральные числа и
Поскольку по условию b и q – натуральные числа и  , где
, где  ,
,  ,
,  . Поскольку по условию b, с, q – натуральные числа и
. Поскольку по условию b, с, q – натуральные числа и  , где
, где  ,
,  ,
,  . Поскольку по условию b, с, d, q – натуральные числа и
. Поскольку по условию b, с, d, q – натуральные числа и  получаем три числа, образующих геометрическую прогрессию: 1, 2, 4, произведение двух оставшихся чисел, отличных от уже найденных, должно быть равно 90. Следовательно, это могут быть числа: 3 и 30, 6 и 15, 9 и 10, 18 и 5.
получаем три числа, образующих геометрическую прогрессию: 1, 2, 4, произведение двух оставшихся чисел, отличных от уже найденных, должно быть равно 90. Следовательно, это могут быть числа: 3 и 30, 6 и 15, 9 и 10, 18 и 5. ,
,  ,
,  ,
, 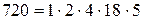 .
.


