Контрольная работа 1

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

Задача 1. Определить скорость скольжения U прямоугольной пластины (а ´ b ´ c) по наклонной плоскости под углом b, если между пластиной и плоскостью находится слой масла А (рисунок 13). Толщина слоя масла d, температура масла Т, плотность материала пластины r. Данные для решения задачи в соответствии с вариантом задания выбрать из таблицы 1.

Указание. При решении задачи применяется формула Ньютона. Поскольку слой масла тонкий, можно считать, что скорость в нем изменяется по прямолинейному закону.

 

Таблица 1

Вариант	Масло	а	b	c	d	r, кг/м3	Т, °С	b°
мм
а	Индустриальное 12				0,5		23,0	6,0
б	Турбинное 30				0,6		35,0	11,0
в	Индустриальное 50				1,3		20,0	13,0
г	Трансформаторное				0,4		25,0	9,0
д	АМГ-10				0,3		22,0	8,0
е	Индустриальное 20				0,8		32,0	13,0
ж	Касторовое				1,4		40,0	8,0
и	Веретенное АУ				0,7		22,0	7,0
к	Индустриальное 30				0,6		25,0	16,0

 

Рисунок 13 Рисунок 14

 

 

Задача 2. Зазор А между валом и втулкой заполнен маслом. Длина втулки L. К валу, диаметр которого D, приложен вращающий момент М (рисунок 14). При вращении вала масло постепенно нагревается и скорость вращения увеличивается. Определить частоту вращения вала при температуре масла Т. Данные для решения задачи в соответствии с вариантом задания выбрать из таблицы 2.

Указание. При решении задачи применяется формула Ньютона. Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; сила трения проходит через центр тяжести этой эпюры.

 

Таблица 2

Вариант	Масло	Т, °С	М, Н × м	d	D	L
мм
а	АМГ-10	46,0	5,10	2,0
б	Индустриальное 25	35,0	27,0	3,0
в	Веретенное АУ	32,0	1,60	1,5
г	Индустриальное 12	37,0	2,10	1,0
д	Турбинное 30	42,0	1,50	1,3
е	Индустриальное 30	27,0	18,0	2,4
ж	Касторовое	76,0	0,140	0,8
и	Индустриальное 50	20,0		3,3
к	Трансформаторное	56,0	1,80	1,2

 

Задача 3. Начальное положение гидравлической системы дистанционного управления представлено на рисунке 15 (рабочая жидкость между поршнями не сжата). При перемещении ведущего поршня (его диаметр D) вправо жидкость постепенно сжимается и давление в ней – повышается. Когда манометрическое давление достигает величины р_м, сила давления на ведомый поршень (его диаметр d ) становится больше силы сопротивления F. С этого момента приходит в движение вправо и ведомый поршень. Диаметр соединительной части цилиндров d, длина l. Определить диаметр ведущего поршня D необходимый для того, чтобы ход L обоих поршней был один и тот же. Данные для решения задачи в соответствии с вариантом задания выбрать из таблицы 3.

Указание. Коэффициент объемного сжатия рабочей жидкости принять b = 0,59 × 10^-9 м²/Н.

Рисунок 15

 

Задача 4. Горизонтальный цилиндрический резервуар (рисунок 16), закрытый полусферическими днищами, заполнен жидкостью Ж. Длина цилиндрической части резервуара L, диаметр D. Манометр М показывает манометрическое давление р_м. Температура жидкости 20°С. Определить силы, разрывающие резервуар по сечениям: 1 – 1, 2 – 2 и 3 – 3. Данные для решения задачи в соответствии с вариантом задания выбрать из таблицы 4.

 

Таблица 3

Вариант	d	L	d	l, м	рм, МПа
мм
а	20,0	30,0	10,0	2,40	21,0
б	18,0	34,0	8,0	2,20	15,0
в	24,0	32,0	12,0	2,00	12,5
г	28,0	36,0	14,0	2,35	17,5
д	20,0	38,5	11,5	1,90	14,0
е	24,5	41,0	12,0	1,75	16,3
ж	28,0	38,5	14,0	1,52	19,1
и	26,0	36,0	8,5	1,61	14,8
к	22,5	34,0	10,5	1,77	17,0

Таблица 4

Вариант	Жидкость, Ж	D	L	рм, МПа
м
а	Вода пресная	1,00	1,50	15,0
б	Керосин Т-1	1,50	2,50	0,00
в	Нефть, Баку, легкая	2,50	3,50	45,0
г	Бензин авиационный	2,00	3,30	21,0
д	Дизельное топливо	2,50	4,00	27,5
е	Керосин Т-2	2,00	3,50	0,00
ж	Нефть, Баку, тяжелая	1,50	2,00	34,2
и	Глицерин	3,00	4,50	26,7
к	Вода пресная	2,50	3,70	18,0

 

Рисунок 16

 

Задача 5. Вертикальная цилиндрическая цистерна (рисунок 17) с полусферической крышкой до самого верха заполнена двумя различными несмешивающимися жидкостями Ж₁ и Ж₂ (соответственно плотности: r₁ и r₂). Диаметр цистерны D, высота ее цилиндрической части Н. Глубина жидкости Ж₁ равна Н/2. Манометр М показывает манометрическое давление р_м. Определить силу, растягивающую болты А и горизонтальную силу, разрывающую цистерну по сечению 1 – 1.

Данные, необходимые для решения задачи, в соответствии с вариантом задания выбрать из таблицы 5.

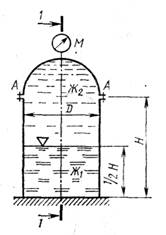
Таблица 5

Вариант	D	Н	r1	r2	рм, кПа
м	Кг/м2
а	2,40	3,90			0,00
б	1,60	3,00			14,2
в	2,80	5,45			11,0
г	1,80	3,60			16,5
д	2,60	4,50			0,00
е	2,00	3,85			21,4
ж	2,20	4,20			27,0
и	1,40	2,80			18,6
к	2,40	4,65			32,0

Рисунок 17

 

Задача 6. Круглое отверстие между двумя резервуарами закрыто конической крышкой с размерами D и L (рисунок 18). Закрытый резервуар заполнен водой, а открытый резервуар – жидкостью Ж.К закрытому резервуару сверху присоединен мановакуумметр МV,показывающийманометрическое давление р_м или величину вакуума р_вак. Температура жидкостей 20°С, глубины h и Н. Определить силу, срезывающую болты А, и горизонтальную силу, действующую на крышку. Данные для решения задачи выбрать в соответствии с вариантом задания из таблицы 6.

Рисунок 18

 

Таблица 6

Вариант	Жидкость, Ж	D	L	h	Н	рм	рвак
мм	м	кПа
а	Нефть Баку, легкая			1,00	1,30	–	24,3
б	Дизельное топливо			1,85	2,20	35,2	–

 

в	Бензин авиационный			1,70	1,90	–	38,6
г	Глицерин			2,00	2,55	24,8	–
д	Керосин Т-1			2,50	3,00	0,00	–
е	Нефть Баку, тяжелая			1,45	1,80	34,4	–
ж	Дизельное топливо			1,30	1,60	29,0	–
и	Бензин авиационный			2,20	2,77	–	28,2
к	Керосин Т-2			2,10	2,50	53,0	–

 

Задача 7. Отливка пустотелых чугунных цилиндров (рисунок 19) высотой Н производится центробежным способом. Во вращающуюся цилиндрическую форму вливаются V литров расплавленного чугуна. Форма вращается со скоростью n, об/мин, ее внутренний диаметр D. Определить толщину стенок отливки сверху и снизу. Данные, необходимые для решения задачи, в соответствии с вариантом задания выбрать из таблицы 7.

Указание. Объемными деформациями металла пренебречь.

 

Таблица 7

Вариант	D	Н	V, л	n, об/мин
мм
а			10,2
б			5,30
в			15,5
г			2,80
д			8,63
е			7,25
ж			17,6
и			4,70
к			8,10

Рисунок 19

Задача 8. Цилиндрический резервуар заполнен жидкостью Ж до высоты 3/4 Н.Диаметр резервуара D, температура жидкости 20°С. Определить (рисунок 20):

1) объем жидкости, сливающийся из резервуара при его вращении с частотой n, об/мин вокруг его вертикальной оси; 2) силу давления на дно резервуара и горизонтальную силу, разрывающую резервуар по сечению 1 – 1 при его вращении. Данные для решения задачи в соответствии с вариантом задания выбрать из таблицы 8.

 

Таблица 8

Вариант	Жидкость, Ж	D	Н	n, об/мин
м
а	Вода пресная	1,00	2,00
б	Нефть Баку, легкая	1,10	1,75
в	Глицерин	1,30	2,20
г	Нефть Баку, тяжелая	1,50	2,45
д	Трансформаторное масло	1,20	1,90
е	Бензин авиационный	1,20	1,50
ж	Вода пресная	1,00	1,40
и	Глицерин	1,20	1,65
к	Дизельное топливо	1,70	1,60

Рисунок 20

 

Задача 9. Сосуд в виде прямоугольного параллелепипеда с размерами L В Н до высоты 2/3 Н заполнен водой, температура которой 20°С. Определить, с каким наибольшим положительным ускорением а может двигаться сосуд по наклонной плоскости под углом a, чтобы вода не выливалась, и какие силы давят на торцовые стенки сосуда в случаях: а) при движении сосуда вниз (рисунок 21, а); б) при движении сосуда вверх (рисунок 21, б).

 

Рисунок 21

 

Данные, необходимые для решения задачи, в соответствии с вариантом задания выбрать из таблицы 9.

Указание. Ускорение а определяется по формуле , где b – угол между поверхностью жидкости и горизонтальной плоскостью; g – ускорение силы тяжести.

 

Таблица 9

Вариант	L	В	Н	a°
м
а	2,00	1,00	1,00
б	1,50	0,90	0,80
в	1,90	1,20	1,10
г	1,60	1,00	0,90
д	1,80	1,10	1,00
е	2,10	1,20	1,10
ж	2,50	1,30	1,20
и	2,20	1,10	1,00
к	2,40	1,20	1,30