Или статическими характеристиками
В практике расчетов устойчивости электрических систем нагрузку часто представляют упрощенно в виде постоянного комплексного сопротивления. Известно, что если мощность приемной системы соизмерима с мощностью электропередачи, то напряжение на шинах нагрузки снижается с увеличением мощности электропередачи. В свою очередь, мощность на сопротивлении нагрузки падает по квадратичной зависимости вплоть до нуля и поэтому всегда можно сбалансировать мощность нагрузки с мощностью генераторов. Следует иметь в виду, что переходные процессы в нагрузке, не нарушая устойчивости самой нагрузки, влияют на режим работы электропередачи и могут быть причиной аварий. В этом случае статическая устойчивость системы оценивается по критерию:
где
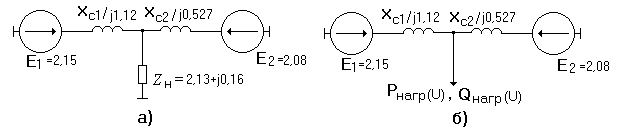
а - принципиальная схема электропередачи; б - схема замещения электропередачи в случае представления нагрузки комплексным постоянным сопротивлением; в - схема замещения электропередачи в случае представления нагрузки статическими характеристиками
Запас устойчивости определяется по максимуму зависимости
где Ро - активная мощность передающей станции в исходном режиме. Если приемная система представлена нагрузкой постоянства ЭДС обеих станций (
где ка, о.е.;
точке
соответствующего генератора до шин нагрузки, о.е. (рис.1 б).
Угловая характеристика активной мощности передающей станции
где соответственно;
ственно. Максимум характеристики (3) дает значение действительного предела мощности передающей станции Таким образом, при представлении нагрузки комплексным постоянным сопротивлением нет необходимости знать характер изменения напряжения на ее шинах. Влияние нагрузки на действительный предел передаваемой мощности проявляется через параметры собственного и взаимного сопротивлений. Для схемы замещения (рис. 1 б) собственное и взаимное сопротивления определяются по формулам: Z Z где Z H - сопротивление нагрузки. Сопротивление нагрузки определяется по формуле: Z H
Статические характеристики комплексной нагрузки представляют собой зависимости активной и реактивной мощности потребителей, входящих в состав нагрузки, от напряжения на шинах нагрузки (рис.2). Рис. 2. Статические характеристики комплексной нагрузки
Для оценки статической устойчивости системы в случае нагрузки, заданной статическими характеристиками, удобно применить критерий:
Решение задачи в данном случае состоит в определении максимума зависимости 1) задаются несколько уменьшенным значением 2) рассчитывают потери
3) по статическим характеристикам (рис.2) определяют
4) рассчитывают ЭДС 5) задаваясь новым увеличенным значением 6) по значению напряжения в точке 1 (рис.3) по статической характеристике (рис.2) определяют соответствующую ей величину 7) задаваясь очередным (уменьшенным) значением
Расчеты ведут до тех пор, пока не будет найден максимум   , являющийся действительным пределом передаваемой активной мощности станции 1. , являющийся действительным пределом передаваемой активной мощности станции 1.
Рис. 3. Зависимость ЭДС
При проведении расчетов следует иметь в виду, что точка 2 на рис. 3 соответствует неустойчивому режиму работы электропередачи (так как угол наклона касательной в этой точке на характеристике Пример 1.. На рис. 4 приведена схема электрической системы, содержащая две генераторные станции, питающие комплексную нагрузку. Требуется: 1) определить коэффициент запаса статической устойчивости по идеальному пределу мощности; 2) построить угловую характеристику активной мощности передающей станции и определить коэффициент запаса статической устойчивости по действительному пределу мощности, представив нагрузку постоянным комплексным сопротивлением; 3) определить коэффициент запаса статической устойчивости по действительному пределу мощности, представив нагрузку статическими характеристиками. Параметры схемы и параметры исходного режима:
Передаваемая мощность станции 1:  50 МВт; 50 МВт;  0,8. 0,8.
Рис.4. Схема электропередачи
Решение. Для определения коэффициента запаса по идеальному пределу мощности принимают, что генератор  отдает мощность в приемную систему несоизмеримо большой мощности. При этих условиях напряжение на шинах нагрузки неизменно по величине и фазе при любых режимах работы электропередачи. На рис. 5 приведена схема замещения для расчета идеального предела мощности. отдает мощность в приемную систему несоизмеримо большой мощности. При этих условиях напряжение на шинах нагрузки неизменно по величине и фазе при любых режимах работы электропередачи. На рис. 5 приведена схема замещения для расчета идеального предела мощности.
Рис.5.Схема замещения для расчета идеального предела мощности Расчет выполним в относительных единицах при базисных условиях:
Параметры схемы замещения и исходного режима при принятых базисных условиях будут:
Сопротивление электропередачи со стороны
ЭДС генераторов передающей станции (
Активная мощность, выдаваемая генератором
Максимум мощности, равный 1,92, может быть назван идеальным пределом активной мощности для станции 1. Коэффициент запаса статической устойчивости по идеальному пределу активной мощности найдем по выражению:
Рис. 6. Схемы замещения электропередачи для расчета действительного предела мощности: а- при нагрузке, заданной постоянным сопротивлением; б- при нагрузке, заданной статическими характеристиками. Сопротивление электропередачи со стороны
Сопротивление комплексной нагрузки согласно (5) будет: Z H где Мощность, поступающая в нагрузку от местной станции
Здесь ЭДС генератора местной станции согласно (2) будет:
Собственное и взаимное сопротивления для станции 1 определим по (4): Z Z Фазные углы собственного и взаимного сопротивлений будут:
Углы потерь собственного и взаимного сопротивлений будут:
Угловая характеристика мощности генератора
Далее вычисляем значения Таблица 1
Рис.7. Угловая характеристика мощности генератора
Максимум этой характеристики дает значение действительного предела активной мощности станции 1:
Коэффициент запаса статической устойчивости системы по действительному пределу мощности будет равен:
Сравнивая значения коэффициентов запаса статической устойчивости по идеальному и действительному пределам мощности, видим, что снижение напряжения на шинах нагрузки за счет представления нагрузки комплексным сопротивлением уменьшает запас статической устойчивости станции 1. Определим действительный предел статической устойчивости станции 1 для случая, когда нагрузка задана статическими характеристиками. Найдем параметры исходного режима (принапряжении на шинах нагрузки
В дальнейшем поступаем в соответствии с алгоритмом расчета, приведенным выше (см. c. 6). Задаемся новыми, меньшими значениями
По статическим характеристикам (рис. 2) для Из условия баланса мощностей в узле нагрузки имеем:
Определяем ЭДС
Замечаем, что По статической характеристике (рис. 2) находим Таким образом, нами была определена вторая точка искомой характеристики Таблица 2
Замечаем, что действительный предел статической устойчивости станции 1 в случае нагрузки, заданной статическими характеристиками, находится в интервале 1,41 - 1,44. Принимая среднее значение
Сопоставляя значения всех найденных пределов статической устойчивости станции 1, заметим, что учет нагрузки по статическим характеристикам дает самое меньшее значение действительного предела, которое наиболее близко к истине.
1.2. Расчет статической устойчивости нагрузки,
|

 ,
, - активная мощность передающей станции;
- активная мощность передающей станции;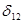 - угол сдвига между векторами ЭДС генераторов
- угол сдвига между векторами ЭДС генераторов  и
и  (рис.1).
(рис.1). 
 при изменяющемся напряжении на нагрузке:
при изменяющемся напряжении на нагрузке: ,(1)
,(1) - максимальная активная мощность передающей станции;
- максимальная активная мощность передающей станции; и местной станцией
и местной станцией  и
и  ), которые определяются по выражению [1]:
), которые определяются по выражению [1]: , (2)
, (2) - напряжение узловой точки системы, к которой подключена нагруз-
- напряжение узловой точки системы, к которой подключена нагруз- - активная и реактивная мощности, поступающие к узловой
- активная и реактивная мощности, поступающие к узловой от соответствующего генератора, о.е.;
от соответствующего генератора, о.е.; - результирующее сопротивление цепи от точки приложения ЭДС
- результирующее сопротивление цепи от точки приложения ЭДС , (3)
, (3) - собственное и взаимное сопротивления передающей станции
- собственное и взаимное сопротивления передающей станции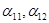 - углы потерь собственного и взаимного сопротивлений соответ-
- углы потерь собственного и взаимного сопротивлений соответ-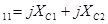 Z H
Z H 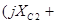 Z H
Z H  ;
; Z H. (4)
Z H. (4) . (5)
. (5)
 .
. при фиксированных значениях ЭДС генераторов (рис.1 б). Так как распределение мощностей от источников в нагрузку при изменении напряжения на ее шинах заранее неизвестно, искомую зависимостьнаходят расчетом, выполняемым в следующей последовательности:
при фиксированных значениях ЭДС генераторов (рис.1 б). Так как распределение мощностей от источников в нагрузку при изменении напряжения на ее шинах заранее неизвестно, искомую зависимостьнаходят расчетом, выполняемым в следующей последовательности: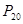 и
и  по сравнению с их значениями в исходном режиме;
по сравнению с их значениями в исходном режиме; в реактивности
в реактивности  и напряжение на шинах нагрузки по выражениям:
и напряжение на шинах нагрузки по выражениям: ; (6)
; (6) ; (7)
; (7) ;
; по (2);
по (2); (рис.3), тангенс угла наклона касательной к которой должен быть больше или равен нулю и чтобы была общая точка пересечения со значением
(рис.3), тангенс угла наклона касательной к которой должен быть больше или равен нулю и чтобы была общая точка пересечения со значением  (например, точка 1 на рис. 3);
(например, точка 1 на рис. 3); и рассчитывают вторую точку искомой зависимости
и рассчитывают вторую точку искомой зависимости 

 ) и поэтому в нашем случае она должна быть отброшена.
) и поэтому в нашем случае она должна быть отброшена. = 1,2;
= 1,2;  = 0,8;
= 0,8;  0,3;
0,3; :
: 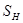 = 63 MBA;
= 63 MBA;  = 10,5 %;
= 10,5 %;  :
: 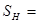 160 МВА;
160 МВА;  12%;
12%; :
:  130МВт;
130МВт; 

 = 50 MBA;
= 50 MBA;  = 115 кВ.
= 115 кВ.


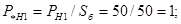




 (8)
(8)
 по действительному пределу мощности составим схемы замещения (рис. 6).
по действительному пределу мощности составим схемы замещения (рис. 6).
 ,
, .
. .
.



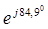 ;
;
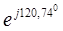 .
. ;
; 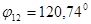 .
. ;
;  .
.
 при других значениях угла
при других значениях угла 





 ) для характерных мест системы (см. рис. 1 в):
) для характерных мест системы (см. рис. 1 в):


 и по (6), (7) рассчитываем:
и по (6), (7) рассчитываем: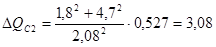 ;
;  .
.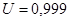 находим:
находим: 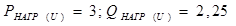 .
.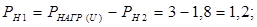

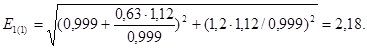
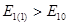 . Поэтому при прежнем значении
. Поэтому при прежнем значении  задаемся новым, несколько увеличенным значением
задаемся новым, несколько увеличенным значением  по сравнению с его величиной в исходном режиме (с целью увеличения потери напряжения в сопротивлении между шинами нагрузки и неизменной ЭДС
по сравнению с его величиной в исходном режиме (с целью увеличения потери напряжения в сопротивлении между шинами нагрузки и неизменной ЭДС  ). Повторив расчет, найдем соответствующее значение
). Повторив расчет, найдем соответствующее значение  . Как видно, заданное значение
. Как видно, заданное значение  находится между найденными величинами
находится между найденными величинами  и
и  , определяя тем самым искомую величину напряжения на шинах нагрузки
, определяя тем самым искомую величину напряжения на шинах нагрузки  (определяется, как точка пересечения прямой, проходящей через найденные значения
(определяется, как точка пересечения прямой, проходящей через найденные значения  с прямой
с прямой  при
при 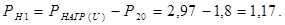


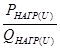
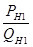








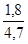












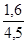









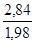



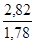



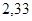





















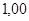



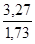




 , определим коэффициент запаса:
, определим коэффициент запаса:



