Порядок виконання завдання 2
1. Запустити програму Microsoft Excel. 2. Побудувати електронну таблицю (завдання 2.1.) та оформити її наступним чином (для формул „правих” та „лівих” прямокутників):
· В клітинці В2 ввести початкове значення діапазону, тобто · В клітинці А6 порахувати значення кроку · Клітинка А6 містить константу – значення кроку, яке постійно використовується для розрахунку значеннь · Порахувати значення · Зробити активною клітину В3, внести в неї формулу для розрахунку функції, використовуючи обраховані раніше значення · В клітинці В4 обрахувати · Клацнувши лівою клавішею миші (ЛКМ) в полі Число 1:, отримуємо в ньому текстовий курсор. Утримуючи ЛКМ у натиснутому стані, виділяємо штриховою лінією діапазон · В клітинці В5 обраховуємо значення відповідного означеного інтегралу =$А$6* В4.
3. Побудувати електронну таблицю (завдання 2.1.) та оформити її наступним чином (для формули „центральних” прямокутників):
· В клітинці В2 ввести початкове значення діапазону, тобто · В клітинці А6 порахувати значення кроку · Клітинка А6 містить константу – значення кроку, яке постійно використовується для розрахунку значеннь · Порахувати значення · Зробити активною клітину В3, внести в неї формулу для розрахунку функції, використовуючи обраховані раніше значення · В клітинці В4 обрахувати · Клацнувши лівою клавішею миші (ЛКМ) в полі Число 1:, отримуємо в ньому текстовий курсор. Утримуючи ЛКМ у натиснутому стані, виділяємо штриховою лінією діапазон · В клітинці В5 обраховуємо значення відповідного означеного інтегралу =$А$6* В4.
4. Побудувати електронну таблицю (завдання 2.1.) та оформити її наступним чином (для формули трапецій):
· В клітинці В2 ввести початкове значення діапазону, тобто · В клітинці А6 порахувати значення кроку · Клітинка А6 містить константу – значення кроку, яке постійно використовується для розрахунку значеннь · Порахувати значення · Зробити активною клітину В3, внести в неї формулу для розрахунку функції, використовуючи обраховані раніше значення · Зробити активною клітину В4, внести в неї формулу =(В3+С3)/2.Формулу із клітини В4 скопіювати в наступні клітини. · В клітинці В4 обрахувати · Клацнувши лівою клавішею миші (ЛКМ) в полі Число 1:, отримуємо в ньому текстовий курсор. Утримуючи ЛКМ у натиснутому стані, виділяємо штриховою лінією діапазон · В клітинці В6 обраховуємо значення відповідного означеного інтегралу =$А$6* В5.
5. Побудувати електронну таблицю (завдання 2.1.) та оформити її наступним чином (для формули Симпсона):
· В клітинці В2 ввести початкове значення діапазону, тобто · В клітинці А6 порахувати значення кроку · Клітинка А6 містить константу – значення кроку, яке постійно використовується для розрахунку значеннь · Порахувати значення · Зробити активною клітину В3, внести в неї формулу для розрахунку функції, використовуючи обраховані раніше значення · Зробити активною клітину В4, внести в неї формулу =(В3+4*С3+D3)/6.Формулу із клітини В4 скопіювати в наступні клітини, де індекс біля x є натуральним числом (тобто 1, 2, 3, 4). · В клітинці В4 обрахувати · Клацнувши лівою клавішею миші (ЛКМ) в полі Число 1:, отримуємо в ньому текстовий курсор. Утримуючи ЛКМ та клавішу Ctrl, виділяємо комірки, що містять суми · В клітинці В6 обраховуємо значення відповідного означеного інтегралу =$А$6* В5.
6. Для побудови графіка функції
7. Зберегти документ на диску з ім’ям zavd2.xls. · Виконати команду Файл→Сохранить как. · У діалоговому вікні Сохранение документа встановити слідуючі параметри: в полі Имя файла ввести zavd2.xls, в списку Папка вибрати робочий диск, у вікні вмісту диску – особисту папку розміщення файлу. Натиснути кнопку Сохранить. 8. Закрити робочу книгу. Вийти із середовища Microsoft Excel. · Виконати команду Файл→Закрыть. · Виконати команду Файл→Выход.
ЗАВДАННЯ №3. ЗНАХОДЖЕННЯ КОРЕНІВ НЕЛІНІЙНИХ РІВНЯНЬ Задано нелінійне рівняння Основні методи відокремлення коренів нелінійних рівнянь. У відповідності з графічним методом необхідно побудувати графік заданої функції Більш зручним слід вважати табличний метод, оскільки він досить формальний і зводиться до послідовності простих обчислювальних операцій. У відповідності з цим методом, на всьому широкому проміжку [А,В] визначають знаки функції Уточнення коренів нелінійних рівнянь. Розглянемо уточнення кореня методом ділення навпіл. Ідея методу полягає в тому, що за один його крок вузький проміжок вдається звузити вдвоє. Для цього достатньо проаналізувати знаки функції Припустимо, що на вузькому проміжку [а,Ь] знаходиться єдиний корінь рівняння При формулюванні алгоритму пошуку кореня нам буде зручно користуватись функцією „знак х”, яка визначається наступним чином:
Алгоритм уточнення:
Знайдене значення кореня доцільно перевірити. Для цього його треба підставити у задане рівняння і обчислити значення функції. Якщо значення функції виявилось близьким до нуля, то значення кореня можна вважати вірним.
3.1.Протабулювати функцію 3.2.Відокремити корені нелінійного рівняння графічним та аналітичним способом (табличним), тобто вказати проміжки, на яких точно є корені. 3.3. Уточнити корені нелінійних рівнянь (методом ділення навпіл). Варіанти: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
|




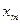





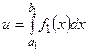
 .
. .
. . Для цього в клітину С2 внести формулу для розрахунку =В2+$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто
. Для цього в клітину С2 внести формулу для розрахунку =В2+$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто  .
. .
.

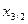




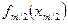


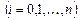 . Для цього в клітину В2 внести формулу для розрахунку =а+0,5*$А$6. Для наступних значень
. Для цього в клітину В2 внести формулу для розрахунку =а+0,5*$А$6. Для наступних значень 

 . Для цього в клітину С2 внести формулу для розрахунку =В2+$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто
. Для цього в клітину С2 внести формулу для розрахунку =В2+$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто 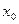

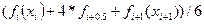

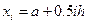 . Для цього в клітину С2 внести формулу для розрахунку =В2+0,5*$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто
. Для цього в клітину С2 внести формулу для розрахунку =В2+0,5*$А$6. Формулу із клітини С2 скопіювати в наступні клітини, доки не досягнемо значення кінця діапазону, тобто  .
. , скористайтесь поясненням до попереднього завдання.
, скористайтесь поясненням до попереднього завдання.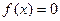 .
. на всьому заданому проміжку [А,В], після чого візуально локалізувати точки його перетину з віссю Ох. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки [а,Ь] так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу - його громіздкість. Другий недолік - ненадійність -пов’язаний з можливістю втратити корені при неякісній побудові графіка.
на всьому заданому проміжку [А,В], після чого візуально локалізувати точки його перетину з віссю Ох. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки [а,Ь] так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу - його громіздкість. Другий недолік - ненадійність -пов’язаний з можливістю втратити корені при неякісній побудові графіка.
 в точці а, тобто
в точці а, тобто 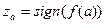 .
. .
. , то вважати
, то вважати 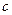 коренем рівняння
коренем рівняння  .
. , то вважати
, то вважати  .
. , то значення b замінити на значення
, то значення b замінити на значення  , то значення a замінити на значення
, то значення a замінити на значення  ;
;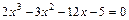 ;
; ;
; ;
; ;
;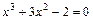 ;
;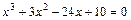 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;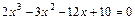 ;
; ;
; ;
; ;
; ;
; ;
; ;
;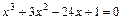 ;
; ;
; ;
;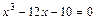 ;
; ;
;


