Справочный материал к контрольной работе по теме
«Интегральное исчисление функции одной переменной» Первообразная и неопределенный интеграл. Таблица интегралов Функция F ( x ) называется первообразной для функции f (x) на интервале (a, b), если для всех x из этого интервала выполняется равенство
Неопределенным интегралом от функции f (x) называется множество всех первообразных этой функции, то есть неопределенный интеграл – это выражение вида Процедуру нахождения неопределенного интеграла называют интегрированием. Таблица интегралов
Свойства неопределенного интеграла. Интегрирование методом подведения под знак дифференциала части подинтегральной функции При интегрировании функций наиболее часто используются следующие его свойства: 1) 2) 3) Пример 1. Найти Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:
Ответ:
Иногда при интегрировании удобно использовать свойство дифференциала:
Пример 2. Найти Решение. Согласно формуле (2) можно записать:
Теперь воспользуемся свойством 2, а также таблицей интегралов:
Инвариантность формул интегрирования позволяет применять при интегрировании подведение под знак дифференциала части подинтегральной функции, основанное на следующей формуле:
Пример 3. Найти Решение. Воспользуемся методом подведения под знак дифференциала, а также таблицей интегралов:
Ответ:
|

 . (1)
. (1) , где
, где  ;
2.
;
2.  ;
3.
;
3. 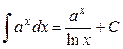 ;
4.
;
4.  ;
5.
;
5.  ;
6.
;
6.  ;
7.
;
7.  ;
8.
;
8. 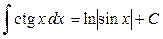 ;
9.
;
9.  ;
;
 ;
11.
;
11. 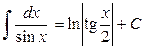 ;
12.
;
12.  ;
13.
;
13.  ;
14.
;
14.  ;
15.
;
15.  ;
16.
;
16.  .
.
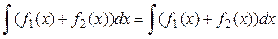 ;
; ;
; .
. .
. =
=  +3
+3  =
=  .
. . (2)
. (2) .
.
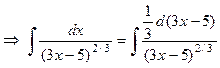 .
.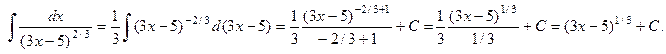 Ответ:
Ответ: 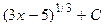 .
. . (3)
. (3) .
. =
=  .
. .
.


