Интегрирование некоторых тригонометрических функций
Для нахождения интегралов видов
Для нахождения интегралов вида
6. Вычисление определенного интеграла по формуле Ньютона–Лейбница Формула Ньютона–Лейбница для вычисления определенного интеграла имеет вид:
если Пример 4. Вычислить определенный интеграл Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона – Лейбница, получаем:
= Ответ: 7. Несобственные интегралы первого и второго рода Интеграл
называется несобственным интегралом первого рода. Интеграл
где a – точка бесконечного разрыва функции Если b – точка бесконечного разрыва функции
– тоже несобственный интеграл второго рода. Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся. Пример 5. Исследовать на сходимость интеграл Решение. Это несобственный интеграл первого рода, поэтому
Следовательно, интеграл сходится и равен Ответ: интеграл сходится и равен Пример 6. Исследовать на сходимость интеграл Решение. Это несобственный интеграл второго рода, так как х = 1 – точка разрыва второго рода подинтегральной функции, поэтому
следовательно, интеграл расходится. Ответ: интеграл расходится. 8. В ычисление площади в декартовой системе координат (ДСК)
Формула для вычисления площади криволинейной трапеции:
y = f 2(x) где
9. В ычисление площади в полярной системе координат (ПСК)
Формула для вычисления площади криволинейного сектора:
10. Вычисление объема тела вращения Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b, y = 0 и непрерывной кривой y = f (x), где
Если криволинейная трапеция ограничена линиями x = a, x= b,
|

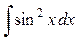 и
и  используют тригонометрические формулы:
используют тригонометрические формулы: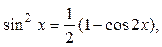
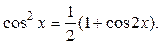 (5)
(5) , где R – рациональная функция (не содержащая sin х и cos x под знаком корней), используют универсальную подстановку:
, где R – рациональная функция (не содержащая sin х и cos x под знаком корней), используют универсальную подстановку: 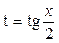 , которая сводит
, которая сводит 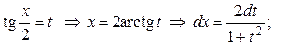 и
и 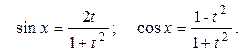 (6)
(6) , (7)
, (7) и
и  непрерывна на
непрерывна на  .
. .
.
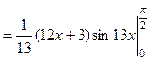
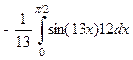
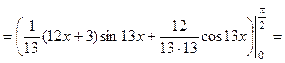
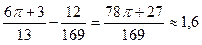 .
.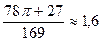 .
. (8)
(8)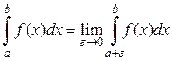 , (9)
, (9)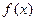 называется несобственным интегралом второго рода.
называется несобственным интегралом второго рода. , (10)
, (10) .
.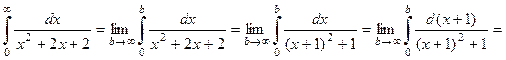

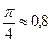 .
. .
.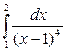
 ,
, Криволинейной трапецией в ДСК называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой y = f (x), где
Криволинейной трапецией в ДСК называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой y = f (x), где  для
для  (рис. 1).
(рис. 1). . (11)
. (11)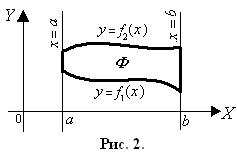 Если фигура Ф ограничена в ДСК линиями x = a, x= b, y = f 1(x) и
Если фигура Ф ограничена в ДСК линиями x = a, x= b, y = f 1(x) и для
для  . (12)
. (12) Криволинейным сектором в ПСК называется фигура, ограниченная лучами
Криволинейным сектором в ПСК называется фигура, ограниченная лучами  и кривой
и кривой 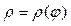 , где
, где  (рис. 3).
(рис. 3). . (13)
. (13)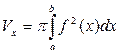 . (14)
. (14) y 1 = f 1(x) и y 2 = f 2(x) где
y 1 = f 1(x) и y 2 = f 2(x) где  . (15)
. (15)


