№ 1
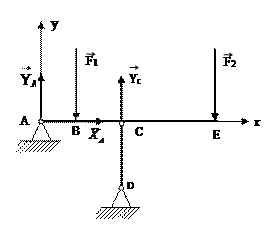
Розглянемо рівновагу балки АЕ. Введемо систем координат Аxy. Звільняємо балку від в’язей та вводимо реакції в’язей:  .
.
Для знаходження реакції стержня записуємо рівняння моментів відносно осі  :
:
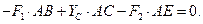
З цього рівняння знаходимо  Н.
Н.
Відповідь:  Н.
Н.
№ 2

Розглянемо рівновагу балки АВ. Введемо систем координат Аxy. Звільняємо балку від в’язей та вводимо реакції в’язей:  .
.
Для знаходження реакції в опорі  записуємо рівняння моментів відносно осі
записуємо рівняння моментів відносно осі  :
:
 .
.
Знаходимо  Н.
Н.
Відповідь:  Н.
Н.
№ 3

Розглянемо рівновагу балки АВ з ниткою та вантажем. Введемо систем координат Вxy. Зображуємо силу  . Звільняємо систему від в’язей та вводимо реакції в’язей:
. Звільняємо систему від в’язей та вводимо реакції в’язей:  . Для знаходження реакцій записуємо рівняння моментів відносно осі
. Для знаходження реакцій записуємо рівняння моментів відносно осі  :
:
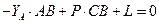
Знаходимо  Н.
Н.
Відповідь:  Н.
Н.
№ 4
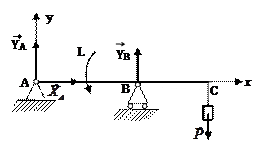
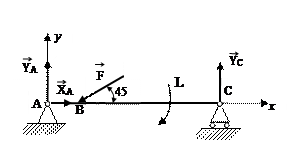
Розглянемо рівновагу балки АС з ниткою та вантажем. Введемо систем координат Аxy. Зображуємо силу  . Звільняємо систему від в’язей та вводимо реакції в’язей:
. Звільняємо систему від в’язей та вводимо реакції в’язей:  . Для знаходження реакцій записуємо рівняння моментів відносно осі
. Для знаходження реакцій записуємо рівняння моментів відносно осі

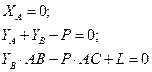
З першого рівняння знаходимо 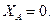
З третього рівняння знаходимо  Н.
Н.
З другого рівняння знаходимо 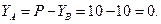
Відповідь:  ,
,  ,
,  Н.
Н.
№ 5
Розглянемо рівновагу балки АС. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей:  . Для знаходження реакції в опорі С записуємо рівняння рівноваги – суму моментів відносно точки А:
. Для знаходження реакції в опорі С записуємо рівняння рівноваги – суму моментів відносно точки А:
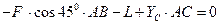
З рівняння знаходимо
 Н.
Н.
Відповідь:  Н.
Н.
№ 6
 Розглянемо рівновагу балки АВ. Введемо систему координат Аxy.. Звільняємо систему від в’язей і вводимо реакції в’язей:
Розглянемо рівновагу балки АВ. Введемо систему координат Аxy.. Звільняємо систему від в’язей і вводимо реакції в’язей:  .
.
Для знаходження реакцій записуємо рівняння рівноваги балки:
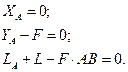
З першого рівняння знаходимо 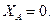
З другого рівняння знаходимо  Н.
Н.
З третього рівняння знаходимо 
 .
.
Відповідь:  ,
,  Н,
Н, 
 .
.
№ 7
 Розглянемо рівновагу балки АВ. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей:
Розглянемо рівновагу балки АВ. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей:  .
.
Для знаходження моменту в защемленні А записуємо рівняння рівноваги балки – суму моментів відносно точки А:
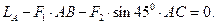
З рівняння знаходимо

 .
.
Відповідь: 
 .
.
№ 8
Нормальне прискорення точки знаходиться за формулою  , де
, де 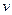 - швидкість точки. За натуральним способом задання руху
- швидкість точки. За натуральним способом задання руху  . Знаходячи
. Знаходячи  , отримаємо
, отримаємо  . В момент часу
. В момент часу  маємо
маємо  , в момент часу
, в момент часу  маємо
маємо  . Тобто
. Тобто  м/с2.
м/с2.
Відповідь:  8 м/с2.
8 м/с2.
№ 9
Прискорення точки знаходиться за формулою  . Дотичне прискорення точки дорівнює
. Дотичне прискорення точки дорівнює  . Нормальне прискорення точки дорівнює
. Нормальне прискорення точки дорівнює  , де
, де 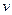 - швидкість точки. За натуральним способом задання руху
- швидкість точки. За натуральним способом задання руху  . Знаходячи
. Знаходячи  м/с, отримаємо
м/с, отримаємо  м/с2 . Прискорення точки дорівнює
м/с2 . Прискорення точки дорівнює  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
№ 10
Доосьове прискорення точки, яка знаходиться на відстані  від точки до осі обертання, дорівнює
від точки до осі обертання, дорівнює  , де
, де  - кутова швидкість обертання тіла, Доосьове прискорення точки, яка знаходиться на відстані
- кутова швидкість обертання тіла, Доосьове прискорення точки, яка знаходиться на відстані  від точки до осі обертання, дорівнює
від точки до осі обертання, дорівнює  тому маємо
тому маємо  . Якщо прийняти
. Якщо прийняти  =2 м/с2,
=2 м/с2,  м,
м,  м, то за цією формулою знаходимо
м, то за цією формулою знаходимо  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
№ 11
Обертальне прискорення точки в момент часу  дорівнює
дорівнює  , де
, де  - відстань від точки до осі обертання. Обертальне прискорення точки в момент часу
- відстань від точки до осі обертання. Обертальне прискорення точки в момент часу  дорівнює
дорівнює  , тобто
, тобто  . Тому
. Тому  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
№ 12
Прискорення точки знаходиться за формулою  . Обертальне прискорення точки дорівнює
. Обертальне прискорення точки дорівнює  , де
, де  - кутове прискорення тіла,
- кутове прискорення тіла,  - відстань від точки до осі обертання. Доосьове прискорення точки дорівнює
- відстань від точки до осі обертання. Доосьове прискорення точки дорівнює  , де
, де  - кутова швидкість обертання тіла. Маємо
- кутова швидкість обертання тіла. Маємо  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
№ 13
 Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде перпендикулярна до кривошипа ОА. Проводимо пряму І1І1, перпендикулярну до вектора
Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде перпендикулярна до кривошипа ОА. Проводимо пряму І1І1, перпендикулярну до вектора 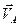 . Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Перетин прямих І1І1 та І2І2 дає миттєвий центр швидкостей – точку Р, яка співпадає з точкою В. Тому
. Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Перетин прямих І1І1 та І2І2 дає миттєвий центр швидкостей – точку Р, яка співпадає з точкою В. Тому  м.
м.
Відповідь:  м.
м.
Завдання № 14
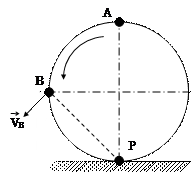
Знайдемо миттєвий центр швидкостей колеса – він знаходиться в точці Р дотику колеса з поверхнею. Вектор  точки В буде напрямлений перпендикулярно до прямої ВР в напрямі обертання колеса. Величину швидкості точки В знайдемо з пропорції
точки В буде напрямлений перпендикулярно до прямої ВР в напрямі обертання колеса. Величину швидкості точки В знайдемо з пропорції  , де R – радіус колеса. Тобто
, де R – радіус колеса. Тобто
 м/c.
м/c.
Відповідь:  м/c.
м/c.
Завдання № 15
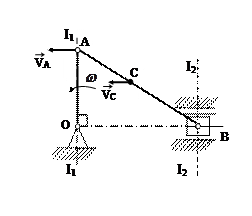
Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І1І1, перпендикулярну до вектора 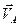 . Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Паралельні прямі І1І1 та І2І2 не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким всі точки тіла мають однакові швидкості. Таким чином,
. Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Паралельні прямі І1І1 та І2І2 не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким всі точки тіла мають однакові швидкості. Таким чином,  . Швидкість точки А, як точки кривошипа ОА, що обертається навколо нерухомої осі, знайдемо за формулою
. Швидкість точки А, як точки кривошипа ОА, що обертається навколо нерухомої осі, знайдемо за формулою  м/c..Таким чином
м/c..Таким чином  м/c.
м/c.
Відповідь: 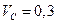 м/c.
м/c.
Завдання № 16
 Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І1І1, перпендикулярну до вектора
Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І1І1, перпендикулярну до вектора 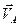 . Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Паралельні прямі І1І1 та І2І2 не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким кутова швидкість шатуна
. Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Паралельні прямі І1І1 та І2І2 не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким кутова швидкість шатуна  дорівнює нулеві.
дорівнює нулеві.
Відповідь:  .
.
Завдання № 17
Шестерня здійснює плоский рух. Для визначення швидкості точки С знайдемо миттєвий центр швидкостей шестерні – він знаходиться в точці Р дотику шестерні до нерухомої поверхні. Далі знаходимо швидкість точки А, яка одночасно належить шестерні та кривошипу. Швидкість точки А напрямлена перпендикулярно до кривошипа в напрямі його обертання і дорівнює  м/с. Зображуємо стрілкою напрям обертання шестерні навколо миттєвого центра
м/с. Зображуємо стрілкою напрям обертання шестерні навколо миттєвого центра  швидкостей. Вектор швидкості точки С буде напрямлений перпендикулярно до відрізку РС в напрямі обертання шестерні, а величину швидкості точки С знайдемо з пропорції
швидкостей. Вектор швидкості точки С буде напрямлений перпендикулярно до відрізку РС в напрямі обертання шестерні, а величину швидкості точки С знайдемо з пропорції  . Таким чином, маємо
. Таким чином, маємо  м/с.
м/с.
Відповідь:  м/c.
м/c.
.
Завдання № 18
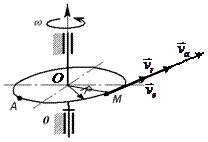
Маємо складний рух точки, за яким абсолютна швидкість  точки
точки  дорівнює
дорівнює  , де
, де  - переносна швидкість,
- переносна швидкість,  - відносна швидкість. Переносна швидкість точки
- відносна швидкість. Переносна швидкість точки  напрямлено перпендикулярно до ОМ в бік обертання тіла, а її величина дорівнює
напрямлено перпендикулярно до ОМ в бік обертання тіла, а її величина дорівнює  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  . В момент часу
. В момент часу  с маємо
с маємо  =1 м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто до ободу диска, а її величина дорівнює
=1 м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто до ободу диска, а її величина дорівнює  м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Напрями переносної та відносної швидкостей співпадають, тому величина абсолютної швидкості точки дорівнює
м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Напрями переносної та відносної швидкостей співпадають, тому величина абсолютної швидкості точки дорівнює  м/c.
м/c.
Відповідь:  м/c.
м/c.
Завдання № 19
 Маємо складний рух точки, за яким абсолютна швидкість
Маємо складний рух точки, за яким абсолютна швидкість  точки
точки  дорівнює
дорівнює  , де
, де  - переносна швидкість,
- переносна швидкість,  - відносна швидкість. Переносна швидкість точки напрямлено перпендикулярно до ОМ в бік обертання тіла, тобто від нас, а її величина дорівнює
- відносна швидкість. Переносна швидкість точки напрямлено перпендикулярно до ОМ в бік обертання тіла, тобто від нас, а її величина дорівнює  , де
, де  . В момент часу
. В момент часу  с маємо
с маємо  м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СВ, а її величина дорівнює 9 м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки
м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СВ, а її величина дорівнює 9 м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки  дорівнює
дорівнює  м/c.
м/c.
Відповідь:  м/c.
м/c.
Завдання № 20

Маємо складний рух точки, за яким абсолютна швидкість  точки
точки  дорівнює
дорівнює  , де
, де  - переносна швидкість,
- переносна швидкість,  - відносна швидкість. Переносна швидкість точки напрямлена перпендикулярно до АМ в бік обертання тіла, тобто до нас, а її величина в момент часу
- відносна швидкість. Переносна швидкість точки напрямлена перпендикулярно до АМ в бік обертання тіла, тобто до нас, а її величина в момент часу  с дорівнює
с дорівнює  м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, а її величина дорівнює
м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, а її величина дорівнює  м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює
м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює  м/c.
м/c.
Відповідь:  м/c.
м/c.
Завдання № 21
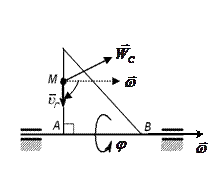
Прискорення Коріоліса точки  визначається за формулою
визначається за формулою  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  - відносна швидкість точки
- відносна швидкість точки  . Кутова швидкість дорівнює
. Кутова швидкість дорівнює  с-1. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, що випливає з додатного значення кутової швидкості. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор
с-1. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, що випливає з додатного значення кутової швидкості. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор  точку М. Вектор
точку М. Вектор  напрямлений так, що з кінця вектора
напрямлений так, що з кінця вектора  найкоротший поворот вектора
найкоротший поворот вектора  до вектора
до вектора  видно проти ходу годинної стрілки, тобто від нас. Модуль вектора
видно проти ходу годинної стрілки, тобто від нас. Модуль вектора  дорівнює
дорівнює  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
Завдання № 22
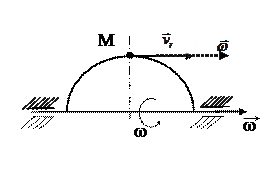
Прискорення Коріоліса точки  визначається за формулою
визначається за формулою  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  - відносна швидкість. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти прискорення Коріоліса, перенесемо вектор
- відносна швидкість. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти прискорення Коріоліса, перенесемо вектор  точку М. Вектори
точку М. Вектори  та
та  напрямлені вздовж однієї прямої, а в цьому випадку модуль вектора
напрямлені вздовж однієї прямої, а в цьому випадку модуль вектора  дорівнює
дорівнює  . Таким чином, прискорення Коріоліса відсутнє.
. Таким чином, прискорення Коріоліса відсутнє.
Відповідь:  .
.
Завдання № 23
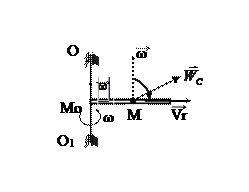
Прискорення Коріоліса точки  визначається за формулою
визначається за формулою  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  - відносна швидкість точки
- відносна швидкість точки  . Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор
. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор  точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж трубки в напрямі руху, а її величина дорівнює
точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж трубки в напрямі руху, а її величина дорівнює  м/c. Щоб знайти прискорення Коріоліса, перенесемо вектор
м/c. Щоб знайти прискорення Коріоліса, перенесемо вектор  точку М. Вектор
точку М. Вектор  напрямлений так, що з кінця вектора
напрямлений так, що з кінця вектора  найкоротший поворот вектора
найкоротший поворот вектора  до вектора
до вектора  видно проти ходу годинної стрілки, тобто від нас. Модуль вектора
видно проти ходу годинної стрілки, тобто від нас. Модуль вектора  дорівнює
дорівнює  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
Завдання № 24
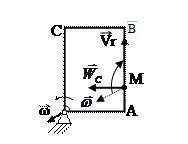
Прискорення Коріоліса точки  визначається за формулою
визначається за формулою  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  - відносна швидкість. точки
- відносна швидкість. точки  . Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, тобто до нас. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор
. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, тобто до нас. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор  точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АВ в напрямі руху, а її величина в момент часу
точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АВ в напрямі руху, а її величина в момент часу  с дорівнює
с дорівнює  м/c. Вектор
м/c. Вектор  напрямлений так, що з кінця вектора
напрямлений так, що з кінця вектора  найкоротший поворот вектора
найкоротший поворот вектора  до вектора
до вектора  видно проти ходу годинної стрілки, тобто вліво. Модуль вектора
видно проти ходу годинної стрілки, тобто вліво. Модуль вектора  дорівнює
дорівнює  м/с2. Звідси знаходимо
м/с2. Звідси знаходимо  с-1.
с-1.
Відповідь:  с-1.
с-1.
Завдання № 25
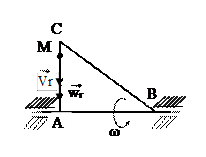
Відносне прискорення точки – це прискорення руху точки в її русі відносно трикутника. Відносне прискорення точки знаходиться за формулою  , де
, де 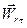 - відносне дотичне прискорення точки,
- відносне дотичне прискорення точки,  - відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює
- відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює  . В момент часу
. В момент часу  =2 с воно дорівнює
=2 с воно дорівнює  м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, і співпадає за напрямом з вектором
м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, і співпадає за напрямом з вектором  , тому що величини
, тому що величини  та
та  мають однаковий знак. Нормальне відносне прискорення точки дорівнює
мають однаковий знак. Нормальне відносне прискорення точки дорівнює  , де
, де  - радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо
- радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо  , тому
, тому  =0. Таким чином
=0. Таким чином  м/с2 .
м/с2 .
Відповідь:  =12 м/с2.
=12 м/с2.
Завдання № 26
 Прискорення Коріоліса точки
Прискорення Коріоліса точки  визначається за формулою
визначається за формулою  , де
, де 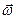 - кутова швидкість тіла,
- кутова швидкість тіла,  - відносна швидкість точки
- відносна швидкість точки  . Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор
. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор 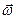 точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СА в напрямі руху, а її величина в момент часу
точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СА в напрямі руху, а її величина в момент часу  с дорівнює
с дорівнює  м/c. Вектор
м/c. Вектор  напрямлений так, що з кінця вектора
напрямлений так, що з кінця вектора  найкоротший поворот вектора
найкоротший поворот вектора 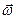 до вектора
до вектора  видно проти ходу годинної стрілки, тобто від нас. Модуль вектора
видно проти ходу годинної стрілки, тобто від нас. Модуль вектора  дорівнює
дорівнює  м/с2.
м/с2.
Відповідь:  м/с2.
м/с2.
Завдання № 27

Відносне прискорення точки – це прискорення руху точки в її русі відносно диска. Відносне прискорення точки знаходиться за формулою  , де
, де 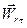 - відносне дотичне прискорення точки,
- відносне дотичне прискорення точки,  - відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює
- відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює  . В момент часу
. В момент часу  =1 с воно дорівнює
=1 с воно дорівнює  м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж діаметра, і співпадає за напрямом з вектором
м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж діаметра, і співпадає за напрямом з вектором  , тому що величини
, тому що величини  та
та  мають однаковий знак. Нормальне відносне прискорення точки дорівнює
мають однаковий знак. Нормальне відносне прискорення точки дорівнює  , де
, де  - радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо
- радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо  , тому
, тому  =0. Таким чином
=0. Таким чином  м/с2 .
м/с2 .
Відповідь:  =12 м/с2.
=12 м/с2.
Задача №28
Запишемо другий закон Ньютона в координатній формі:  , тобто
, тобто 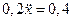 . Звідси знаходимо прискорення точки:
. Звідси знаходимо прискорення точки:  м/с2. Інтегруючи цей вираз, отримаємо:
м/с2. Інтегруючи цей вираз, отримаємо:
 м/с.
м/с.
Відповідь: 10 м/с.
Задача №29
Запишемо другий закон Ньютона в координатній формі:  , тобто 0,
, тобто 0,  . Звідси знаходимо прискорення точки:
. Звідси знаходимо прискорення точки:  м/с2. Інтегруючи цей вираз при нульових початкових умовах, отримаємо:
м/с2. Інтегруючи цей вираз при нульових початкових умовах, отримаємо:
 м.
м.
Відповідь: 12 м.
Задача №30
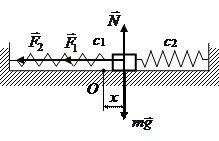
Розглянемо рух тіла вздовж поверхні. На нього діють сили: сила ваги  , сили пружності пружин
, сили пружності пружин  та
та  , та реакція поверхні
, та реакція поверхні  . В координатній формі в проекції на вісь
. В координатній формі в проекції на вісь  рівняння руху має вигляд:
рівняння руху має вигляд:
 .
.
Перепишемо його так:
 ,
,
де  - частота власних коливань.
- частота власних коливань.
Знаходимо:
 1/с
1/с
Відповідь: 10 1/с.
Задача №31
Будемо розглядати рух кульки. Зобразимо сили, що на неї діють – це сила ваги  та натяг нитки
та натяг нитки  .
.  Зобразимо нормаль
Зобразимо нормаль  , яка напрямлена до шарніра О, та швидкість точки
, яка напрямлена до шарніра О, та швидкість точки  , яка напрямлена перпендикулярно до нитки.
, яка напрямлена перпендикулярно до нитки.
Запишемо другий закон Ньютона в проекції на нормаль:  Звідси отримаємо вираз для натягу нитки:
Звідси отримаємо вираз для натягу нитки:
 Н.
Н.
Відповідь: 1 Н.
Задача №32
Будемо розглядати рух кульки. Зобразимо сили, що на неї діють – це сила ваги  та натяг нитки
та натяг нитки  .
.  Зобразимо нормаль
Зобразимо нормаль  , яка напрямлена до шарніра О, та швидкість точки
, яка напрямлена до шарніра О, та швидкість точки  , яка напрямлена перпендикулярно до нитки.
, яка напрямлена перпендикулярно до нитки.
Запишемо другий закон Ньютона в проекції на нормаль:
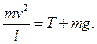
Звідси отримаємо вираз для натягу нитки:
 Н.
Н.
Відповідь: 1,02 Н.
Задача №33

Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  та реакція мосту
та реакція мосту  , яку направимо протилежно нормалі
, яку направимо протилежно нормалі  до поверхні мосту. Вектор швидкості автомобіля направимо по дотичній до поверхні мосту.
до поверхні мосту. Вектор швидкості автомобіля направимо по дотичній до поверхні мосту.
Запишемо другий закон Ньютона в проекції на нормаль:
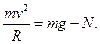
Звідси отримаємо вираз для реакції мосту:
 Н.
Н.
Відповідь:8800 Н.
Задача №34
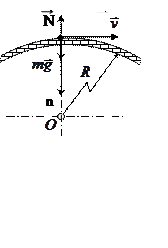
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  та реакція мосту
та реакція мосту  , яку направимо протилежно нормалі
, яку направимо протилежно нормалі  до поверхні мосту. Вектор швидкості автомобіля направимо по дотичній до поверхні мосту.
до поверхні мосту. Вектор швидкості автомобіля направимо по дотичній до поверхні мосту.
Запишемо другий закон Ньютона в проекції на нормаль:
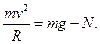
Покладаючи  , знаходимо:
, знаходимо:
 м/с.
м/с.
Відповідь: 20 м/с.
Задача №35
 Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  , реакція поверхні
, реакція поверхні  та сила тертя
та сила тертя  .
.
Запишемо другий закон Ньютона в проекції на нормаль:
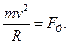
Знаходимо:
 Н
Н
Відповідь: 4000 Н.
Задача №36
 Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  , реакція поверхні
, реакція поверхні  та сила тертя
та сила тертя  .
.
Використаємо теорему про зміну кінетичної енергії матеріальної точки:
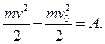
Маємо:
 .
.
Знаходимо:  . Початкова швидкість автомобіля дорівнює:
. Початкова швидкість автомобіля дорівнює:  м/с
м/с
Тоді
 м
м
Відповідь: 50 м.
 Задача №37
Задача №37
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  , сила тертя
, сила тертя  та нормальна реакція поверхні
та нормальна реакція поверхні  . Запишемо рівняння руху тіла
. Запишемо рівняння руху тіла  . Сила тертя дорівнює
. Сила тертя дорівнює  , де
, де  - коефіцієнт тертя. Для знаходження реакції опори запишемо другий закон Ньютона в проекції на вісь
- коефіцієнт тертя. Для знаходження реакції опори запишемо другий закон Ньютона в проекції на вісь  :
:  . Тобто,
. Тобто,  . Тобто,
. Тобто,  . Виконаємо інтегрування:
. Виконаємо інтегрування:  ,
,  - сталі інтегрування. Для їх знаходження запишемо початкові умови:
- сталі інтегрування. Для їх знаходження запишемо початкові умови:  . Будемо мати
. Будемо мати  . Таким чином, будемо мати
. Таким чином, будемо мати  ,
,  . Час, який тіло буде рухатися до зупинки знаходиться з умови
. Час, який тіло буде рухатися до зупинки знаходиться з умови  . Маємо
. Маємо  . Тоді шлях до зупинки буде дорівнювати:
. Тоді шлях до зупинки буде дорівнювати: 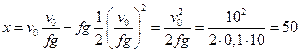 м.
м.
Відповідь: 50 м.
 Задача №38
Задача №38
Зобразимо сили, які діють на ротор – це сила ваги  та реакції опори
та реакції опори  . Запишемо рівняння руху ротора навколо осі обертання
. Запишемо рівняння руху ротора навколо осі обертання  :
:  , де
, де 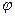 - кут повороту ротора,
- кут повороту ротора,  осьовий момент інерції. Для диска маси M і радіуса
осьовий момент інерції. Для диска маси M і радіуса  маємо
маємо  . Тобто
. Тобто
 с-2.
с-2.
При нульових початкових умовах кутова швидкість в момент  с дорівнює:
с дорівнює:  с-1.
с-1.
Відповідь: 20


 .
. :
: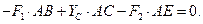
 Н.
Н. Н.
Н.
 .
. записуємо рівняння моментів відносно осі
записуємо рівняння моментів відносно осі  .
. Н.
Н. Н.
Н.
 . Звільняємо систему від в’язей та вводимо реакції в’язей:
. Звільняємо систему від в’язей та вводимо реакції в’язей:  . Для знаходження реакцій записуємо рівняння моментів відносно осі
. Для знаходження реакцій записуємо рівняння моментів відносно осі  :
: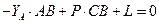
 Н.
Н. Н.
Н.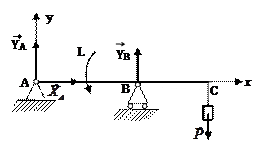

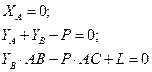
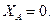
 Н.
Н.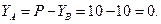
 ,
,  ,
,  Н.
Н.
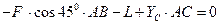
 Н.
Н. Н.
Н. Розглянемо рівновагу балки АВ. Введемо систему координат Аxy.. Звільняємо систему від в’язей і вводимо реакції в’язей:
Розглянемо рівновагу балки АВ. Введемо систему координат Аxy.. Звільняємо систему від в’язей і вводимо реакції в’язей:  .
.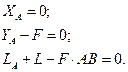
 Н.
Н.
 .
. Н,
Н, 
 Розглянемо рівновагу балки АВ. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей:
Розглянемо рівновагу балки АВ. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей: 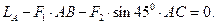


 , де
, де 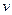 - швидкість точки. За натуральним способом задання руху
- швидкість точки. За натуральним способом задання руху  . Знаходячи
. Знаходячи  , отримаємо
, отримаємо  . В момент часу
. В момент часу  маємо
маємо  , в момент часу
, в момент часу  маємо
маємо  . Тобто
. Тобто  м/с2.
м/с2. 8 м/с2.
8 м/с2. . Дотичне прискорення точки дорівнює
. Дотичне прискорення точки дорівнює  . Нормальне прискорення точки дорівнює
. Нормальне прискорення точки дорівнює  , де
, де  м/с, отримаємо
м/с, отримаємо  м/с2 . Прискорення точки дорівнює
м/с2 . Прискорення точки дорівнює  м/с2.
м/с2. м/с2.
м/с2. від точки до осі обертання, дорівнює
від точки до осі обертання, дорівнює  , де
, де  - кутова швидкість обертання тіла, Доосьове прискорення точки, яка знаходиться на відстані
- кутова швидкість обертання тіла, Доосьове прискорення точки, яка знаходиться на відстані  від точки до осі обертання, дорівнює
від точки до осі обертання, дорівнює  тому маємо
тому маємо  . Якщо прийняти
. Якщо прийняти  =2 м/с2,
=2 м/с2,  м,
м,  м, то за цією формулою знаходимо
м, то за цією формулою знаходимо  м/с2.
м/с2. м/с2.
м/с2. , де
, де  - відстань від точки до осі обертання. Обертальне прискорення точки в момент часу
- відстань від точки до осі обертання. Обертальне прискорення точки в момент часу  , тобто
, тобто  . Тому
. Тому  м/с2.
м/с2. м/с2.
м/с2. . Обертальне прискорення точки дорівнює
. Обертальне прискорення точки дорівнює  , де
, де  - кутове прискорення тіла,
- кутове прискорення тіла,  - відстань від точки до осі обертання. Доосьове прискорення точки дорівнює
- відстань від точки до осі обертання. Доосьове прискорення точки дорівнює  , де
, де  м/с2.
м/с2. м/с2.
м/с2. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде перпендикулярна до кривошипа ОА. Проводимо пряму І1І1, перпендикулярну до вектора
Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде перпендикулярна до кривошипа ОА. Проводимо пряму І1І1, перпендикулярну до вектора 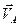 . Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Перетин прямих І1І1 та І2І2 дає миттєвий центр швидкостей – точку Р, яка співпадає з точкою В. Тому
. Вектор швидкості точки В завжди напрямленийвздовж напрямних, які обмежують рух повзуна – проводимо пряму І2І2, перпендикулярну до напрямних. Перетин прямих І1І1 та І2І2 дає миттєвий центр швидкостей – точку Р, яка співпадає з точкою В. Тому  м.
м. м.
м.
 точки В буде напрямлений перпендикулярно до прямої ВР в напрямі обертання колеса. Величину швидкості точки В знайдемо з пропорції
точки В буде напрямлений перпендикулярно до прямої ВР в напрямі обертання колеса. Величину швидкості точки В знайдемо з пропорції  , де R – радіус колеса. Тобто
, де R – радіус колеса. Тобто м/c.
м/c. м/c.
м/c.
 . Швидкість точки А, як точки кривошипа ОА, що обертається навколо нерухомої осі, знайдемо за формулою
. Швидкість точки А, як точки кривошипа ОА, що обертається навколо нерухомої осі, знайдемо за формулою  м/c..Таким чином
м/c..Таким чином  м/c.
м/c.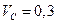 м/c.
м/c. Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І1І1, перпендикулярну до вектора
Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І1І1, перпендикулярну до вектора  дорівнює нулеві.
дорівнює нулеві. .
. м/с. Зображуємо стрілкою напрям обертання шестерні навколо миттєвого центра
м/с. Зображуємо стрілкою напрям обертання шестерні навколо миттєвого центра  швидкостей. Вектор швидкості точки С буде напрямлений перпендикулярно до відрізку РС в напрямі обертання шестерні, а величину швидкості точки С знайдемо з пропорції
швидкостей. Вектор швидкості точки С буде напрямлений перпендикулярно до відрізку РС в напрямі обертання шестерні, а величину швидкості точки С знайдемо з пропорції  . Таким чином, маємо
. Таким чином, маємо  м/с.
м/с. м/c.
м/c.
 точки
точки  дорівнює
дорівнює  , де
, де  - переносна швидкість,
- переносна швидкість,  - відносна швидкість. Переносна швидкість точки
- відносна швидкість. Переносна швидкість точки  , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла, 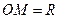 . В момент часу
. В момент часу  с маємо
с маємо  =1 м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто до ободу диска, а її величина дорівнює
=1 м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто до ободу диска, а її величина дорівнює  м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Напрями переносної та відносної швидкостей співпадають, тому величина абсолютної швидкості точки дорівнює
м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Напрями переносної та відносної швидкостей співпадають, тому величина абсолютної швидкості точки дорівнює  м/c.
м/c. м/c.
м/c. Маємо складний рух точки, за яким абсолютна швидкість
Маємо складний рух точки, за яким абсолютна швидкість  , де
, де  . В момент часу
. В момент часу  с маємо
с маємо  м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СВ, а її величина дорівнює 9 м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки
м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СВ, а її величина дорівнює 9 м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки  м/c.
м/c. м/c.
м/c.
 с дорівнює
с дорівнює  м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, а її величина дорівнює
м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, а її величина дорівнює  м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює
м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює 
 , де
, де  - кутова швидкість тіла,
- кутова швидкість тіла,  с-1. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, що випливає з додатного значення кутової швидкості. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор
с-1. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, що випливає з додатного значення кутової швидкості. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор  напрямлений так, що з кінця вектора
напрямлений так, що з кінця вектора  м/с2.
м/с2. м/с2.
м/с2.
 . Таким чином, прискорення Коріоліса відсутнє.
. Таким чином, прискорення Коріоліса відсутнє. .
.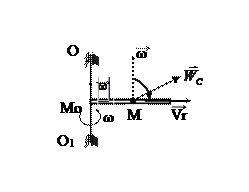
 м/c. Щоб знайти прискорення Коріоліса, перенесемо вектор
м/c. Щоб знайти прискорення Коріоліса, перенесемо вектор  м/с2.
м/с2. м/с2.
м/с2.
 с дорівнює
с дорівнює  м/c. Вектор
м/c. Вектор  м/с2. Звідси знаходимо
м/с2. Звідси знаходимо  с-1.
с-1. с-1.
с-1.
 , де
, де  - відносне дотичне прискорення точки,
- відносне дотичне прискорення точки,  - відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює
- відносне нормальне прискорення точки. Відносне дотичне прискорення точки дорівнює  . В момент часу
. В момент часу  =2 с воно дорівнює
=2 с воно дорівнює  м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, і співпадає за напрямом з вектором
м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, і співпадає за напрямом з вектором  та
та  мають однаковий знак. Нормальне відносне прискорення точки дорівнює
мають однаковий знак. Нормальне відносне прискорення точки дорівнює  , де
, де  - радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо
- радіус кривини траєкторії руху точки в момент визначення цього прискорення. При відносному русі вздовж прямої маємо  , тому
, тому  м/с2 .
м/с2 . =12 м/с2.
=12 м/с2. Прискорення Коріоліса точки
Прискорення Коріоліса точки  м/c. Вектор
м/c. Вектор  м/с2.
м/с2. м/с2.
м/с2.
 . В момент часу
. В момент часу  м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж діаметра, і співпадає за напрямом з вектором
м/с2. Воно напрямлена по дотичній до траєкторії відносного руху, тобто вздовж діаметра, і співпадає за напрямом з вектором  , тобто
, тобто 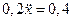 . Звідси знаходимо прискорення точки:
. Звідси знаходимо прискорення точки:  м/с2. Інтегруючи цей вираз, отримаємо:
м/с2. Інтегруючи цей вираз, отримаємо: м/с.
м/с. . Звідси знаходимо прискорення точки:
. Звідси знаходимо прискорення точки:  м/с2. Інтегруючи цей вираз при нульових початкових умовах, отримаємо:
м/с2. Інтегруючи цей вираз при нульових початкових умовах, отримаємо: м.
м.
 , сили пружності пружин
, сили пружності пружин  та
та  , та реакція поверхні
, та реакція поверхні  . В координатній формі в проекції на вісь
. В координатній формі в проекції на вісь  рівняння руху має вигляд:
рівняння руху має вигляд: .
. ,
, - частота власних коливань.
- частота власних коливань. 1/с
1/с .
.  Зобразимо нормаль
Зобразимо нормаль  , яка напрямлена до шарніра О, та швидкість точки
, яка напрямлена до шарніра О, та швидкість точки  , яка напрямлена перпендикулярно до нитки.
, яка напрямлена перпендикулярно до нитки. Звідси отримаємо вираз для натягу нитки:
Звідси отримаємо вираз для натягу нитки: Н.
Н. Зобразимо нормаль
Зобразимо нормаль 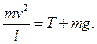
 Н.
Н.
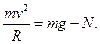
 Н.
Н.
 , знаходимо:
, знаходимо: м/с.
м/с. Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги  .
.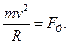
 Н
Н Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги
Будемо розглядати автомобіль як матеріальну точку, на яку діють сила ваги 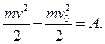
 .
. . Початкова швидкість автомобіля дорівнює:
. Початкова швидкість автомобіля дорівнює:  м/с
м/с м
м Задача №37
Задача №37 та нормальна реакція поверхні
та нормальна реакція поверхні  . Сила тертя дорівнює
. Сила тертя дорівнює  , де
, де  - коефіцієнт тертя. Для знаходження реакції опори запишемо другий закон Ньютона в проекції на вісь
- коефіцієнт тертя. Для знаходження реакції опори запишемо другий закон Ньютона в проекції на вісь  :
:  . Тобто,
. Тобто,  . Тобто,
. Тобто,  . Виконаємо інтегрування:
. Виконаємо інтегрування:  ,
,  - сталі інтегрування. Для їх знаходження запишемо початкові умови:
- сталі інтегрування. Для їх знаходження запишемо початкові умови:  . Будемо мати
. Будемо мати  . Таким чином, будемо мати
. Таким чином, будемо мати  ,
,  . Час, який тіло буде рухатися до зупинки знаходиться з умови
. Час, який тіло буде рухатися до зупинки знаходиться з умови  . Маємо
. Маємо  . Тоді шлях до зупинки буде дорівнювати:
. Тоді шлях до зупинки буде дорівнювати: 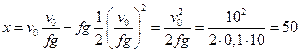 м.
м. Задача №38
Задача №38 та реакції опори
та реакції опори  . Запишемо рівняння руху ротора навколо осі обертання
. Запишемо рівняння руху ротора навколо осі обертання  :
:  , де
, де  - кут повороту ротора,
- кут повороту ротора,  осьовий момент інерції. Для диска маси M і радіуса
осьовий момент інерції. Для диска маси M і радіуса  . Тобто
. Тобто с-2.
с-2. с-1.
с-1.


