Ранний период (зарождение дисциплины) XVII - XIX вв.
Тема 1. Формы правления в зарубежных странах (на примерах США, Франции, Германии, Японии, Испании, Китая) - 2 часа
План 1. Понятие формы правления. 2. Причины многообразия форм правления. 3. Монархия: понятие и виды, порядок престолонаследия: n абсолютная монархия; n конституционная (ограниченная) монархия: президентская (дуалистическая), парламентарная; n “выборная” монархия. 4. Республика: понятие и виды, различия между ними: n президентская республика; n смешанная (полупрезидентская) республика; n парламентарная республика; n особенности республиканской формы правления в социалистических и развивающихся странах с однопартийной системой.
Литература и нормативный материал
1. Арановский К.В. Курс лекций по государственному праву зарубежных стран. Сравнительное государствоведение - Владивосток: Изд-во Дальневосточного ун-та, 1996. 2. Государственный строй КНР. - М., 1988. 3. Иностранное конституционное право. Учебное пособие / Под ред. В.В. Маклакова. - М. 1996. 4. Керимов А.Д. Парламентское представительство как средство контроля за исполнительным правом // Государство и право. 1992. № 7. 5. Конституции зарубежных государств. - М.: БЕК, 1996. 6. Конституционное (государственное) право зарубежных стран. Учебник / Под ред. Б.А. Страшуна. - М.: БЕК, 1997. Т.1, 2. 7. Новые конституции стран Восточной Европы и Азии 1989-1992. Сборник конституций. - М., 1996. 8. Осавелюк А.М. Современный механизм системы сдержек и противовесов в зарубежных странах // Государство и право. 1993. № 12. 9. Сравнительное конституционное право. - М.: Манускрипт, 1996. 10. Урьянс Ю.П. Политический механизм ФРГ. - М.: Наука, 1991. 11. Энтин Л.М. Разделение властей: опыт современных государств. - М., 1995.
Тема 2. Политико-территориальное устройство в зарубежных странах (сравнительный анализ по текстам конституций США, ФРГ, Швейцарии, Испании, Китая) - 2 часа
План 1. Территориальное устройство государства: понятие, формы. 2. Унитарное государство: n децентрализованные унитарные государства; n относительно децентрализованные унитарные государства; n централизованные унитарные государства; 3. Федерация, ее понятие. 4. Конституционно-правовой статус субъектов федерации и иных носителей государственной автономии. 5. Порядок распределения компетенции и отношения между федерацией и ее субъектами. 6. Порядок разрешения конфликтов между федерацией и субъектами. 7. Правовой статус федеральных территорий и зависимых территорий.
Литература и нормативный материал
1. Домрин А. Федеральная интервенция в дела субъектов федерации. Зарубежный опыт правового регулирования и практика применения // Независимая газета. 1995. 28 февраля. 2. Конституции зарубежных государства. - М.: БЕК, 1996. 3. Конституции социалистических государств. - М., 1987. 4. Конституционное (государственное) право. Учебник / Под ред. Б.А. Страшуна. - М.: БЕК, 1997. 5. Крылов Б.С. США: федерализм, штаты и местное самоуправление. - М.: Наука, 1968. 6. Современные зарубежные конституции: Сборник документов. - М., 1992. 7. Федерация в зарубежных странах. - М.: Юрид. лит., 1993. 8. Чиркин В.Е. Модели современного федерализма // Государство и право. 1994. № 8. Примечание. При раскрытии вопросов работа с текстами конституций обязательна.
ВАРИАНТ 1 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 2 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 3
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 4
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 5
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 6
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 7
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда:
ВАРИАНТ 8
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 9
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) б) в) 5. Найти область сходимости степенного ряда:
ВАРИАНТ 10
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 1 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 2 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 3
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 4
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 5
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 6
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 7
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда:
ВАРИАНТ 8
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 9
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) б) в) 5. Найти область сходимости степенного ряда:
ВАРИАНТ 10
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 1 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 2 1. Найти приближённо изменение данной функции 2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 3
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 4
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 5
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 6
2. Найти 3. Решить задачу Коши и сделать проверку: 4. Решить дифференциальные уравнения: а) в) 5. Найти область сходимости степенного ряда: ВАРИАНТ 7
2. Найти
|

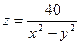 при изменении
при изменении  от
от  до
до  , а
, а  от
от  до
до 
 ,
,  ,
,  , если
, если 
 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 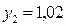

 ,
, 
 б)
б) 
 ,
, 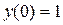 ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 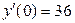

 при изменении
при изменении  до
до  , а
, а  до
до 

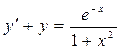 ,
, 
 б)
б) 
 ,
, 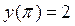 ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

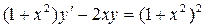 ,
, 
 б)
б) 
 ,
, 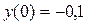 ,
, 

 при изменении
при изменении  до
до  , а
, а 

 ,
, 
 б)
б) 
 ,
,  ,
, 
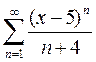
 при изменении
при изменении  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 
 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а 

 ,
, 


 ,
, 
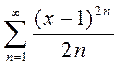
 при изменении
при изменении  , а
, а 

 ,
, 
 б)
б) 
 ,
,  ,
, 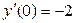

 при изменении
при изменении  от
от  до
до  , а
, а  от
от  до
до 
 ,
,  ,
,  , если
, если 
 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 
 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а 

 ,
, 


 ,
, 

 при изменении
при изменении  , а
, а 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  от
от  до
до  , а
, а  от
от  до
до 
 ,
,  ,
,  , если
, если 
 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а  до
до 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  до
до  , а
, а 

 ,
, 
 б)
б) 
 ,
,  ,
, 

 при изменении
при изменении  , а
, а  до
до 



