ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СЕРВИСА» Кафедра: «Высшая математика»
КОНТРОЛЬНАЯ РАБОТА
По дисциплине: «Математика»
Работу выполнил студент гр. Проверил:
Тольятти 2012 г.
Содержание Задача 1…………………………………………………………………….4 Задача 2…………………………………………………………………….5 Задача 3…………………………………………………………………….6-7 Задача 4…………………………………………………………………….8 Задача 5…………………………………………………………………….9 Задача 6……………………………………………………………………10 Задача 7……………………………………………………………………11-14 Задача 8……………………………………………………………………15 Задача 9……………………………………………………………………16-17 Задача 10…………………………………………………………………..18-21 Литература………………………………………………………………..22 Задача 1. В ящике находятся Решение: Рассмотрим: событиеA – две извлечённые наудачу перчатки образуют пару черного цвета; событиеВ – две извлечённые наудачу перчатки образуют пару бежевого цвета. P (A) = P (B) =
Искомая вероятность: P=P (A) + P (B) =
или P = Так как P= P(A) + P(B) =
Ответ: Задача 2. В урне находятся 3 шара белого цвета и а) ровно два белых шара; б) не менее двух белых шаров. Решение: Рассмотрим событие P(A1)= P(A2)= P(A3)= а) вероятность того, что среди извлеченных шаров окажется ровно два белых шара: P = б) вероятность того, что среди извлеченных шаров окажется не менее двух белых шаров: P = Так как В урне находятся 3 шара белого цвета и 3 шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется: а) ровно два белых шара; б) не менее двух белых шаров. а) P = б) P =
Ответ: Задача 3. В урне находятся Решение: Рассмотрим событие
По формуле полной вероятности:
Так как В урне находятся 5 белых и 4 черных шара. Последовательно извлекаются наудачу три шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.
По формуле полной вероятности:
Ответ: Задача 4. Число деталей, выпущенных на первом заводе, относится к числу деталей, выпущенных на втором заводе как Решение: Пусть:
событие тогда:
Искомую вероятность найдем по формуле Бейеса:
Ответ:
Задача 5. Среди учебников 30% старых. Вероятность того, что в старом учебнике есть все темы лекционного курса, равна 0,8. В новых учебниках отражены все темы лекционного курса с вероятностью 0,52. Учебник содержит все темы лекционного курса. Какова вероятность того, что этот учебник новый? Решение: Пусть:
событие тогда:
Искомую вероятность найдем по формуле Бейеса:
Ответ: Задача 6-4. Закон распределения дискретной случайной величины
Найти вероятности Решение: 1. Найдём вероятности Зная, что
2. Дисперсию найдём по формуле:
Ответ: 1.
2. Задача 7-5. Плотность распределения непрерывной случайной величины Х имеет вид:
Найти: а) параметр б) функцию распределения в) вероятность попадания случайной величины Х в интервал (4;6); г) математическое ожидание M (X) и дисперсию D (X); д) построить графики функций f(x) и F(x). Решение:
|


 одинаковых пар перчаток черного цвета и
одинаковых пар перчаток черного цвета и  одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.
одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару. ;
; .
.
 .
.
 , имеем:
, имеем:
 .
. .
. шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:
шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется: – при
– при  – ом извлечении достают белый шар.
– ом извлечении достают белый шар. ; P
; P  .
. .
. .
. 

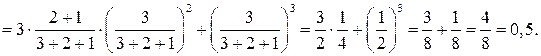

 белых и
белых и  ;
; 
 ;
;  ;
;  ;
; 
 ;
;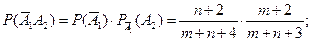


 ;
;  ;
;  ;
;  .
.
 ;
; ;
; ;
; ;
; ;
;
 ;
;


 ;
; ;
; ;
; .
.
 .
. . Вероятность выпуска годной детали на первом заводе равна 0,06, а для второго завода эта вероятность равна 0,3. Все детали поступают на один склад. Какова вероятность того, что наугад взятая со склада деталь будет годной?
. Вероятность выпуска годной детали на первом заводе равна 0,06, а для второго завода эта вероятность равна 0,3. Все детали поступают на один склад. Какова вероятность того, что наугад взятая со склада деталь будет годной? – гипотезы, состоящие в выборе соответственно детали, выпущенной на первом заводе и на втором заводе;
– гипотезы, состоящие в выборе соответственно детали, выпущенной на первом заводе и на втором заводе; – наугад взятая со склада деталь будет годной.
– наугад взятая со склада деталь будет годной. ;
; ;
; - (вероятность выпуска годной детали на первом заводе);
- (вероятность выпуска годной детали на первом заводе); - (вероятность выпуска годной детали на втором заводе).
- (вероятность выпуска годной детали на втором заводе).
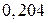 .
. ;
; ;
; - (вероятность того, что в старом учебнике есть все темы лекционного курса);
- (вероятность того, что в старом учебнике есть все темы лекционного курса); - (вероятность того, что в новом учебнике есть все темы лекционного курса).
- (вероятность того, что в новом учебнике есть все темы лекционного курса).
 .
. имеет вид:
имеет вид:





 , дисперсию
, дисперсию  , если математическое ожидание равно:
, если математическое ожидание равно:  .
. , имеем:
, имеем:  ;
; ;
; ;
;  ;
; .
.
 .
.

 ;
; ;
;


