Контрольная работа. по дисциплине: математические методы в психологии
по дисциплине: математические методы в психологии факультет менеджмента и психологи группа ПЗСС12 В 5
Подготовил: Трудов Д. Ю. Проверил: к. ф-м н. Махмудов Н.Р.
Калуга 2015 Задание 1 Две группы пациентов оценивались по стобальной шкале. Определить: значимо ли отличаются средние показатели первой группы от аналогичный показателей второй.
n=11 x =∑x/n; x =581/11=52,82 y =∑y/n; y =737/11=67
дисперсия: Dx=δ x 2=∑(xi- x)2/(n-1); Dx=1377,61/10=137,76 Dу=δ у 2=∑(yi- y)2/(n-1); Dу=3826/10=382,6 Коэффициент Стьюдента tэ=| x - y |/√((Dx/n)+(Dy/n)); t=(67-52,82)/√(137,76+382,6)/11=14,18/6,88=2,06 число степеней свободы: f=n+n-2; f=11+11-2=20 определяем по таблице коэффициент Стьюдента (tт) при f=20; α=0,05=> tт=2,086
2,086>2,06; tт>tэ Различие коэффициентов не существенно. Следовательно, выборки относятся к одной генеральной совокупности. Задание 2 Найти линейную зависимость между y и x методом наименьших квадратов.
a∑xi+nb; ∑yi
6.8a+5b=46
y1=0,7*3.0402+5.0653=7.19344 y2=0,9*3.0402+5.0653=7.80148 y3=1,3*3.0402+5.0653=9.01756 y4=1,6*3.0402+5.0653=9.93 y5=2,3*3.0402+5.0653=12.058
Задание 3 Дано распределение случайной величины x. Найти математическое ожидание и среднее квадратичное отклонение.
δ(x)=√D(x); D(x)=M[x2]-[M(x)]2
Математическое ожидание:
δ(x)=√D(x); D(x)=M(x2)-(M(x))2=> δ(x)=√ 6.4+1.2+0.4+1.8-0.42=√9.64≈3.1
Задание 4
q=5; p=3 Общая выборочная дисперсия: Sобщ=Sф2+Sост2 Введем/рассмотрим для удобства общую сумму квадратичных отклонений от общей среды:
Так же, факторную сумму квадратов отклонений групповых средних от общих:
Rобщ=(7544+7343+8242)*5*3*392=23129-22815=314
Отсюда: Rф=q∑((xj2) -p(x)2) Rф=5*(38,42+38,22+40,42-3*392)=5*(1474,56+1459,24+1632,16-3*1521)= =5*2,96=14,8 Rост=Rобщ-Rф=314-14,8=299,2 Sф2=Rф/(p-1)=14,8/2=7,4 Sост2=Rост/(p(q-1))=299,2/12≈24,93 Наблюдаемая дисперсия: fнабл= Sф2 /Sост2=7,4/24,93≈ 0,297 Используя таблицу распределения Фишера-Снедекора, при k1=2 и k2=12 при уровне значимости α=0,05, найдем fкрит (0,05)= 3,88. Так как fнабл< fкрит, значит, можно не учитывать влияние фактора на качество объекта. Нет оснований отвергнуть нулевую гипотезу. Задание 5 Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины:
P(Y=4)=0.06+0.18+0.24=0.48 => M(X| Y=4)=2*0.06/0.48+3*0.18/0.48+5*0.24/0.48= 3.875 P(Y=6)=0.12+0.13+0.27=0.52 => M(X| Y=6)=2*0.12/0.52+3*0.13/0.52+5*0.27/0.52= 3.8077
Задание 6 Для приведение данных вычислить среднее арифметическое, дисперсию и среднее квадратичное отклонение:
δ=√8,61=2,934 Задание 7 По приведенным значениям IQ (по Векслеру) у родителей и детей определить коэффициент корреляции Пирсона между уровнем интеллекта родителей и детей.
τ=(∑xy-(∑x∑y)/n)/√(∑x2-∑x2/n) (∑y2-∑y2/n)
τ=(125698-(1116*1126)/10)/ √(125162-11162/10)(127552-11262/10)
τ=36,4/√471176,2)=36.4/686,4227=0,53029
Задание 7 Расcчитать и построить гистограмму относительных частот по сгруппированным данным, где m2 – частоты попадания вариант в промежуток (xi;xi+1)
Длина интервала h=2; Относительные частоты: Wi=mi/m Плотность относительных частоты: Wi/h
|

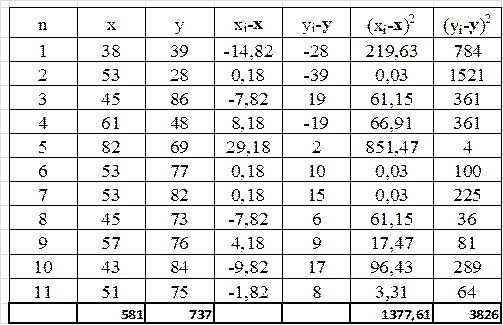
 Представление линейной зависимости: y=ax+b
Представление линейной зависимости: y=ax+b
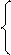
 a∑ xi2+b∑xi; ∑yixi
a∑ xi2+b∑xi; ∑yixi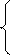 10.84a+6.8b=67.4
10.84a+6.8b=67.4 a=∆1/∆ a=4.2/7.96≈3.04
a=∆1/∆ a=4.2/7.96≈3.04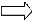 b=∆2/∆ b=40.32/7.96≈5.0653
b=∆2/∆ b=40.32/7.96≈5.0653 y=ax+b y=3.04*x+5.0653
y=ax+b y=3.04*x+5.0653 При уровне значимости α=0,05 методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта на основании пяти измерений для трех уровней фактора:
При уровне значимости α=0,05 методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта на основании пяти измерений для трех уровней фактора:






