Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение

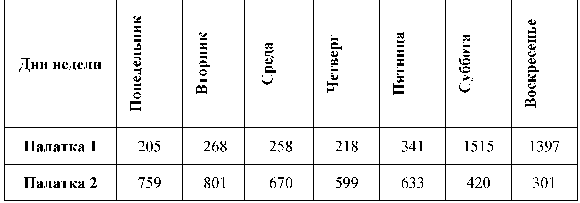
Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение

Вероятно, Вы отлично знаете, что такое среднее арифметическое. Если мы имеем набор каких-то величин, и все они одной природы (усреднять килограммы с километрами мы, конечно, не можем), надо посчитать сумму, а затем, поделив ее на количество слагаемых, найти среднее арифметическое. Казалось бы, простое и хорошо знакомое действие, но и тут имеется несколько проблем для обсуждения. При знакомстве с некоторыми "показателями" поневоле вспоминается известная шутка о "средней температуре по больнице".

Пример. Допустим, фирма имеет две палатки, торгующие горячей выпечкой, которую они пекут на месте из полуфабрикатов. В таблице приводится примерная сводка ежедневной выручки каждой из палаток за неделю (в руб.).

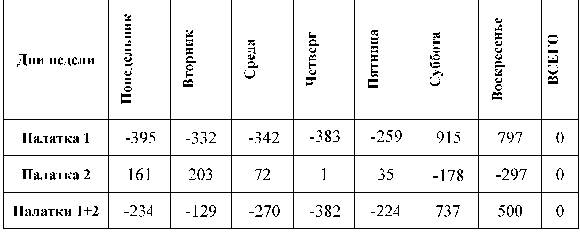
Различие в ежедневной выручке в основном связано с расположением палаток. Палатка 1 находится в парке отдыха, в то время как Палатка 2 расположена напротив школы и вблизи проходной крупного НИИ.

Владелец фирмы решил выплачивать ежемесячную премию продавцам той палатки, которая даст в этом месяце большую выручку. При распределении премии выяснилась удивительная вещь: выигрыш в этом "соревновании" зависел только от количества выходных в месяце.

Не хотелось бы приводить большое количество цифр за весь месяц в целом, но и без этого видно, что если бы владельцу фирмы пришла в голову идея ежедневного премирования победителя какой-то фиксированной суммой, "Палатка выходного дня" могла бы рассчитывать на премии в два с половиной раза реже, хотя недельная выручка от нее больше.

В таких условиях более разумное соревнование могло бы быть основано на осреднении показателей за неделю. Допустим, недельные показатели практически совпали. Как оценить, какая из палаток полезнее для фирмы, если по каким-то причинам фирме необходимо продать одну из них?

Если выручка практически совпадает, владелец, по-видимому, поинтересуется стабильностью работы торговой точки. Вины продавцов в этом нет, но если оборудование работает два дня в неделю на износ, а в остальное время больше простоев, выход из строя такого оборудования более вероятен. Пусть в один (случайным образом выпавший) день в неделю идет сильный дождь, и на улицах мало прохожих, падение выручки особенно резко заметно, когда такой дождливый день совпадает с одним из выходных. Для сравнения можно представить спортсменов, которые имеют равные шансы выиграть, но один из них выступает ровнее. Скорее всего, именно он и будет принят в состав сборной.

Но вот еще один вопрос: а не делает ли эта самая нестабильная палатка работу фирмы в целом более стабильной, прекрасно дополняя работу палатки 2? Давайте выдвинем это утверждение в качестве гипотезы и попробуем его доказать или опровергнуть. Чтобы оценить эту проблему количественно, надо прежде всего просуммировать дневную выручку обеих палаток.

То, что мы описали общими словами как "нестабильность работы", в статистике называется характеристикой рассеивания. К ним относятся такие показатели как дисперсия и среднее квадратическое отклонение. Покажем на предыдущем примере, как определяются эти понятия. Посчитаем сначала среднее арифметическое выручки для каждой палатки отдельно, и для обеих палаток вместе (осреднение проводим за семь дней):

Х_ср.1=600 руб., Х_ср.2=598 руб., Х_ср.1+2=1198 руб.

Чтобы сравнить разброс значений, посчитаем для обеих палаток дневные отклонения выручки от их собственного среднего значения.

Чтобы измерить, насколько одна палатка "нестабильнее" другой, хочется сложить всю строку за неделю и получить общее отклонение за весь отчетный период. Но этого делать нельзя, мы сами так построили эти показатели, что, сложив, получим ноль (с точностью до погрешности округления - среднее арифметическое величина не обязательно целая). Чтобы избежать этого обнуления, нам надо, чтобы каждое отклонение от среднего арифметического "лишилось" своего знака. Для этого возводят каждую величину в квадрат, и лишь затем суммируют весь ряд значений.

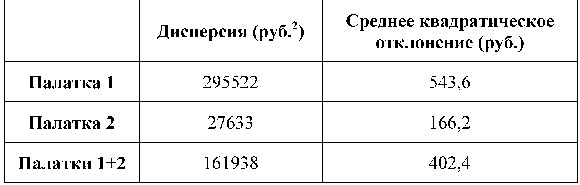
Чтобы не зависеть от периода осреднения делят полученную сумму квадратов на число слагаемых (в нашем случае, по-прежнему на семь). Такая величина называется дисперсией.

Мы видим, что дисперсия действительно очень показательная величина. У "Палатки выходного дня" она выше более, чем в десять раз. Дисперсию можно посчитать в Excel автоматически, даже не считая предварительно среднее арифметическое, программа сделает это сама. Для этого, находясь в файле Excel, нажмите в верхнем меню кнопку f_x. Затем, выберите среди функций тип "СТАТИСТИЧЕСКИЕ", и из предложенного перечня в окошке - ДИСПРА. Затем, по подсказке, поставив курсор в поле "Число 1" проведите мышью вдоль строки с набранными значениями. Этот вид подсчета называется "вычисление смещенной дисперсии по генеральной совокупности". Дисперсией часто пользуются, но более удобная характеристика носит название среднее квадратическое отклонение (обычно обозначается греческой буквой омега. Среднее квадратическое отклонение - это квадратный корень из дисперсии, он удобен тем, что имеет ту же размерность, что и исходные величины. Так, в нашем случае, дисперсия имела бы размерность "рубли в квадрате", в то время как среднее квадратическое отклонение получается просто и привычно, в рублях. В нашем примере, видно, что суммарная дисперсия и среднее квадратическое отклонение у двух палаток вместе все-таки выше, чем у одной первой палатки, причем среднее квадратическое отклонение выше более, чем в два раза. Значит, наша гипотеза о "повышенной стабильности суммы" за счет присутствия второй палатки несостоятельна. Иногда, вместо среднего арифметического употребляют другие характерные величины, если это по каким-то причинам лучше описывает выборку. Так если расставить выборку по возрастанию (или убыванию) той величины, которой мы интересуемся, то медиана - это то, что будет ровно посередине "строя". Например, если мы расположим по порядку длительности интервалы времени: секунда, минута, час, сутки и неделя - то медианой будет час. Еще одно понятие для замены среднего - мода. Само название позволяет легко запомнить это определение. Если мы выстроим по порядку все пары обуви на складе по размеру, то самый ходовой размер будет модой. Мода - это то, что непременно должны учитывать производители упаковок и фасовщики. Если бы большинство людей покупало за один раз стакан молока, молочные пакеты не были бы литровыми. В следующем параграфе мы начнем работать со случайными величинами, имеющими нормальное распределение, и эти понятия нам снова встретятся.