Предварительная математическая обработка статистических данных
После получения результатов эксперимента для дальнейшего их анализа проводится упорядочение данных, их графическое представление и расчет основных числовых характеристик. Наблюдаемые значения исследуемого признака Х называют вариантами и обозначают Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. К характеристикам вариационного ряда относятся: 1) Размах варьирования R — это разность между наибольшим 2) Мода Мо — это варианта, имеющая наибольшую частоту; 3) Медиана Ме — это варианта, делящая вариационный ряд пополам по числу вариант. Статистическим распределением выборки называют множество вариант и соответствующих им частот. Обычно статистическое распреде-ление выборки представляют в виде таблицы:
Эмпирической функцией распределения называется числовая функция
где
Основными графическими формами представления данных наблюдений являются полигон частот и гистограмма. Полигоном частот называется ломаная линия, звенья которой соединяют точки с координатами Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы одинаковой длины h, а высотами — плотности интервальных частот Основными характеристиками выборки являются: 1) Выборочная средняя
2) Выборочная дисперсия
3) Исправленная дисперсия
4) Выборочное среднее квадратическое отклонение
5) Исправленное среднее квадратическое отклонение s, вычисляется по формуле:
6) Коэффициент вариации V, вычисляется по формуле:
Перечисленные характеристики относятся к точечным оценкам, при малых объёмах выборки предпочтительнее пользоваться интервальными оценками. Доверительным интервалом для параметра Например, в случае нормально распределённой случайной величины доверительный интервал для среднего значения при неизвестном параметре
где t — критическая точка распределения Стьюдента с Пример. Статистическая обработка результатов измерений (вычисления выполнять с точностью до двух знаков после запятой) Даны результаты измерений значений случайной величины Х. Составить статистическое распределение выборки и найти: а) характеристики вариационного ряда: размах варьирования, моду, медиану; б) эмпирическую функцию распределения и построить ее график; в) построить полигон частот и гистограмму; г) выборочную среднюю; д) выборочную и исправленную дисперсии; е) выборочное и исправленное средние квадратические отклонения (стандарт); ж) коэффициент вариации (%); з) доверительный интервал для среднего значения признака Х с надежностью 12; 9; 16; 17; 10; 9; 15; 12; 15;16; 20; 18; 17; 9; 15; 9; 16; 9; 18; 16 Составим статистическое распределение выборки. Для этого расположим варианты в порядке возрастания: 9; 9; 9; 9; 9; 10; 12; 12; 15; 15; 15; 16; 16; 16; 16; 17; 17; 18; 18; 20 и подсчитаем числа наблюдений каждой варианты — частоты. Получим:
а) Размах варьирования б) Эмпирическую функцию распределения найдём по формуле (1):
Построим график (рис. 1)
в) Построим полигон частот (рис. 2). Для этого по оси
Для построения гистограммы разобьём интервал изменения x (9,20) на два интервала одинаковой длины h =5,5, подсчитаем интервальные частоты и плотности интервальных частот. Результаты внесём в таблицу 1. Таблица 1
Построим гистограмму (рис. 3).
г) Вычислим выборочную среднюю по формуле (2):
д) Вычислим выборочную дисперсию формуле (3):
Исправленную дисперсию найдём по формуле (4):
е) Выборочное и исправленное средние квадратические отклонения найдём по формулам (5) и (6):
ж) Коэффициент вариации вычислим по формуле (7):
з) Доверительный интервал для среднего значения признака Х найдём по формуле (8). Сначала по таблице [1] найдём критическую точку распределения Стьюдента с числом степеней свободы
|

 , числа их наблюдений называют частотами и обозначают
, числа их наблюдений называют частотами и обозначают  Общее число наблюдений называют объёмом выборки и обозначают n,
Общее число наблюдений называют объёмом выборки и обозначают n, 
 и наименьшим
и наименьшим  значениями,
значениями, 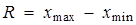 ;
;




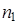


 , определяющая относительную частоту события
, определяющая относительную частоту события  Она вычисляется по формуле:
Она вычисляется по формуле: (1)
(1) — сумма частот вариант, значения которых меньше х, n — объём выборки.
— сумма частот вариант, значения которых меньше х, n — объём выборки. является неубывающей функцией, значения которой принадлежат отрезку
является неубывающей функцией, значения которой принадлежат отрезку  .
.  , определяющей вероятность события
, определяющей вероятность события  ,
,  , …,
, …,  .
. .
. , вычисляется по формуле:
, вычисляется по формуле: . (2)
. (2) , вычисляется по формуле:
, вычисляется по формуле: . (3)
. (3) , вычисляется по формуле:
, вычисляется по формуле: (4)
(4) , вычисляется по формуле:
, вычисляется по формуле: (5)
(5) (6)
(6) . (7)
. (7) , точечной оценкой которого является
, точечной оценкой которого является  , называют интервал
, называют интервал  , содержащий с заданной вероятностью
, содержащий с заданной вероятностью 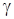 значение параметра
значение параметра  называют надежностью оценки.
называют надежностью оценки. определяется формулой:
определяется формулой: (8)
(8)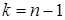 степенями свободы для двусторонней области на уровне значимости
степенями свободы для двусторонней области на уровне значимости  определяется по таблицам, например в
определяется по таблицам, например в  .
.
 мода Мо =9; объём выборки n =20, поэтому середина вариационного ряда находится между 10-й и 11-й вариантами в упорядоченном вариационном ряду, и медиана вычисляется как их среднее арифметическое, Ме = (15+15)/2=15.
мода Мо =9; объём выборки n =20, поэтому середина вариационного ряда находится между 10-й и 11-й вариантами в упорядоченном вариационном ряду, и медиана вычисляется как их среднее арифметическое, Ме = (15+15)/2=15.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
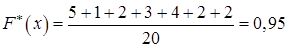 ;
;


 отложим наблюдаемые значения
отложим наблюдаемые значения  , а по оси
, а по оси  частоты
частоты  . Отметим точки с координатами
. Отметим точки с координатами  и соединим их последовательно отрезками прямых.
и соединим их последовательно отрезками прямых.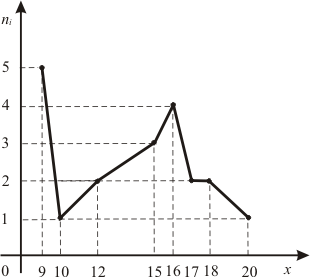
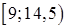


 .
. .
.


 и уровнем значимости
и уровнем значимости  Получим t = 2,09 и подставим в формулу (8):
Получим t = 2,09 и подставим в формулу (8): . После вычисления получим доверительный интервал для среднего значения
. После вычисления получим доверительный интервал для среднего значения 



