Вычисление ошибок косвенных измерений
В большинстве случаев в ходе эксперимента несколькими приборами измеряются несколько величин и для получения конечного результата эти измерения необходимо обработать, используя математические операции: сложения, умножения и т.д. Поэтому необходимо оценивать точность опыта в целом с помощью вычисления предельной и среднеквадратической ошибок опыта. Правила вычисления предельной относительной ошибки опыта: 1. Ошибка суммы заключена между наибольшей и наименьшей из относительных ошибок слагаемых. Обычно учитывается или наибольшая ошибка или средняя арифметическая величина (в лабораторной работе будем пользоваться средней арифметической величиной). 2. Ошибка произведения или частного равна сумме относительных ошибок сомножителей или соответственно делимого и делителя. 3. Ошибка n -ой степени основания в n раз больше относительной ошибки основания. Для вычисления среднеквадратической ошибки результата косвенных измерений необходимо обеспечить независимость результатов измерений. В этом случае среднеквадратическая ошибка вычисления величины W, являющейся функцией измеряемых прямо параметров x, y, z, …
где Пример. Определение погрешности косвенных измерений В результате многократных измерений были получены средние значения и среднеквадратические ошибки 3-х взаимно независимых параметров: Найти: а) предельную относительную ошибку измерений б) среднее значение и среднеквадратическую ошибку определения функции
а) Найдём предельные относительные ошибки измерений x, y, z по формуле (13):
Предельную относительную ошибку определения функции
б) Вычислим среднее значение функции
Для вычисления среднеквадратической ошибки определения функции
и вычислим их при средних значениях x, y, z:
Подставляя в формулу (14), получим:
4. Расчёт характеристик линейной регрессионной модели Одним из эффективных методов установления взаимосвязей между факторами является корреляционно-регрессионный анализ. Задача корреляционно-регрессионного метода заключается в нахождении эмпирического уравнения, характеризующего связь результативного параметра Y c определённым входным фактором Х. В качестве формы связи Y и X широко используют линейную зависимость в силу её простоты в расчётах, а также в связи с тем, что к ней можно привести многие другие виды зависимости. Расчёт линейной регрессионной модели включает следующие этапы: 1. Расчёт теоретического уравнения линейной регрессии; 2. Оценка силы связи, расчёт коэффициента корреляции; 3. Оценка значимости коэффициента корреляции; 4. Оценка значимости коэффициентов уравнения регрессии; 5. Определение адекватности уравнения регрессии и доверительных границ. Линейная регрессия Y на X имеет вид:
где α и β — параметры регрессии (β называется коэффициентом регрессии). Статистические оценки Оптимальные значения параметров, полученные согласно этому методу, определяются формулами:
где
Учитывая (15), запишем эмпирическую линию регрессии в виде:
Силу линейной корреляционной зависимости Y и X характеризует коэффициент корреляции r. Коэффициент r изменяется в пределах от
Коэффициент корреляции
Критическое значение t -критерия Для оценки параметров, входящих в уравнение регрессии (16), при решении практических задач можно ограничиться построением доверительных интервалов. Для заданной надёжности γ доверительные интервалы для параметров
где
После получения эмпирического уравнения регрессии, проверяют насколько оно соответствует результатам наблюдений. Для проверки гипотезы о значимости уравнения регрессии используют F -критерий Фишера, наблюдаемое значение которого вычисляют по формуле:
где
Критическое значение F -критерия Ещё одной характеристикой меры того, насколько эмпирическое уравнение хорошо описывает данную систему наблюдений, является коэффициент детерминации d, который вычисляется по формуле:
Чем ближе коэффициент d к единице, тем лучше описание. После того как модель построена, она используется для анализа и прогноза. Прогноз осуществляется подстановкой фактора
Доверительный интервал для прогнозируемого значения имеет вид:
где Пример. Построение модели линейной регрессии По данным наблюдений определить параметры линейного уравнения регрессии Y на X. Найти коэффициенты регрессии и корреляции проверить гипотезу о значимости выборочного коэффициента корреляции. Найти доверительные интервалы для параметров уравнения регрессии. Определить коэффициент детерминации. Проверить гипотезу о значимости полученного уравнения регрессии. Найти прогнозируемое моделью значение y при x=x 0 и найти для него доверительный интервал. Уровень значимости
Для получения параметров уравнения регрессии составим таблицу. Таблица 2
В последней строке таблицы приведены суммы столбцов, используемых в расчётах. Найдём средние значения X и Y по формуле (16):
Вычислим коэффициент регрессии по формуле (15):
По формуле (28) вычислим теоретические значения Вычислим коэффициент корреляции по формуле (18):
Для определения доверительных интервалов параметров уравнения линейной регрессии (28) найдём остаточную дисперсию по формуле (22):
Доверительный интервал для
Проверим гипотезу о значимости полученного уравнения регрессии. Для вычисления наблюдаемого значения F -критерия найдём исправленную дисперсию Y по формуле (24): Для оценки адекватности линейной модели наблюдаемым значениям найдём также коэффициент детерминации по формуле (25):
Используем уравнение (28) для прогноза. При Окончательно, интервальная оценка для
|

 определяется формулой:
определяется формулой:
 (14)
(14) — частные производные функции
— частные производные функции 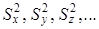 — исправленные дисперсии соответственно x, y, z, ….
— исправленные дисперсии соответственно x, y, z, ….





 и предельную относительную ошибку определения функции
и предельную относительную ошибку определения функции 



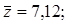





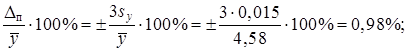










 и
и  параметров регрессии α и β выбираются таким образом, чтобы значения
параметров регрессии α и β выбираются таким образом, чтобы значения  вычисленные по формуле
вычисленные по формуле  были как можно ближе к эмпирическим значениям
были как можно ближе к эмпирическим значениям  . В качестве меры близости выбирают сумму квадратов отклонений
. В качестве меры близости выбирают сумму квадратов отклонений  . Метод нахождения параметров с помощью минимизации суммы квадратов отклонений эмпирических значений
. Метод нахождения параметров с помощью минимизации суммы квадратов отклонений эмпирических значений  в тех же точках называют методом наименьших квадратов.
в тех же точках называют методом наименьших квадратов. (15)
(15) и
и  — средние значения X и Y, которые вычисляют по формулам:
— средние значения X и Y, которые вычисляют по формулам:
 (16)
(16) (17)
(17) до 1. Чем ближе он к
до 1. Чем ближе он к  , тем сильнее линейная связь Y и X, в предельном случае, если
, тем сильнее линейная связь Y и X, в предельном случае, если  , имеет место точная линейная функциональная зависимость Y от X. Если
, имеет место точная линейная функциональная зависимость Y от X. Если  , то Y и X не коррелируют. Оценкой коэффициента корреляции r служит выборочный коэффициент корреляции
, то Y и X не коррелируют. Оценкой коэффициента корреляции r служит выборочный коэффициент корреляции  , который вычисляется по формуле:
, который вычисляется по формуле: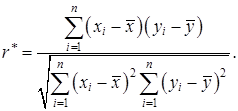 (18)
(18) определяемый по выборочным данным, может не совпадать с действительным значением, соответствующим генеральной совокупности. Для проверки статистической гипотезы о значимости выборочного коэффициента корреляции используют t -критерий Стьюдента, наблюдаемое значение которого вычисляется по формуле:
определяемый по выборочным данным, может не совпадать с действительным значением, соответствующим генеральной совокупности. Для проверки статистической гипотезы о значимости выборочного коэффициента корреляции используют t -критерий Стьюдента, наблюдаемое значение которого вычисляется по формуле: (19)
(19) для числа степеней свободы
для числа степеней свободы  и уровня значимости α находят по таблицам критических точек распределения Стьюдента [1]. Если
и уровня значимости α находят по таблицам критических точек распределения Стьюдента [1]. Если  , то предположение о нулевом значении коэффициента корреляции не подтверждается, и выборочный коэффициент корреляции значим. Если
, то предположение о нулевом значении коэффициента корреляции не подтверждается, и выборочный коэффициент корреляции значим. Если  , то величина r близка к нулю.
, то величина r близка к нулю. и β определяются формулами:
и β определяются формулами: (20)
(20) (21)
(21) — критическое значение t -критерия для числа степеней свободы
— критическое значение t -критерия для числа степеней свободы  , которое находят по таблицам критических точек распределения Стьюдента [1],
, которое находят по таблицам критических точек распределения Стьюдента [1],  — квадратный корень из остаточной дисперсии
— квадратный корень из остаточной дисперсии  , которая находится по формуле:
, которая находится по формуле: . (22)
. (22) (23)
(23) — исправленная дисперсия Y, которая вычисляется по формуле:
— исправленная дисперсия Y, которая вычисляется по формуле: (24)
(24) для числа степеней свободы
для числа степеней свободы  и
и  и уровня значимости α находят по таблицам критических точек распределения Фишера-Снедекора [1]. Если
и уровня значимости α находят по таблицам критических точек распределения Фишера-Снедекора [1]. Если  , то гипотеза о незначимости уравнения регрессии не подтверждается, и уравнение соответствует результатам наблюдений. Если
, то гипотеза о незначимости уравнения регрессии не подтверждается, и уравнение соответствует результатам наблюдений. Если  , то полученное уравнение незначимо.
, то полученное уравнение незначимо. (25)
(25) в уравнение (17). Получается точечная оценка
в уравнение (17). Получается точечная оценка  :
: (26)
(26) (27)
(27) принять равным 0,05.
принять равным 0,05.



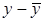





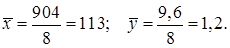
 и получим эмпирическое уравнение регрессии, подставляя
и получим эмпирическое уравнение регрессии, подставляя  в (17):
в (17): (28)
(28) и проверим гипотезу о его значимости. Наблюдаемое значение критерия найдём по формуле (19):
и проверим гипотезу о его значимости. Наблюдаемое значение критерия найдём по формуле (19): По таблице критических точек распределения Стьюдента [1] найдём критическую точку распределения Стьюдента с числом степеней свободы
По таблице критических точек распределения Стьюдента [1] найдём критическую точку распределения Стьюдента с числом степеней свободы  и уровнем значимости
и уровнем значимости  Получим
Получим  и сравним
и сравним  и
и  :
:  следовательно, коэффициент корреляции значим, и Y и X связаны линейной корреляционной зависимостью.
следовательно, коэффициент корреляции значим, и Y и X связаны линейной корреляционной зависимостью. Подставляя в формулу (20), получим доверительный интервал для
Подставляя в формулу (20), получим доверительный интервал для 
 Вычисляя, получим интервальную оценку для
Вычисляя, получим интервальную оценку для 

 получим по формуле (21):
получим по формуле (21): Итак, интервальная оценка для параметра
Итак, интервальная оценка для параметра 

 Подставляя в формулу (23), получим:
Подставляя в формулу (23), получим:  По таблице критических точек распределения Фишера-Снедекора [1] для числа степеней свободы
По таблице критических точек распределения Фишера-Снедекора [1] для числа степеней свободы  и
и 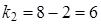 на уровне значимости
на уровне значимости  найдём
найдём  Сравнивая наблюдаемое и критическое значения F -критерия, получим
Сравнивая наблюдаемое и критическое значения F -критерия, получим  следовательно, уравнение значимо.
следовательно, уравнение значимо. Этот результат истолковывается так: 97,1% изменчивости Y объясняется изменением фактора X, а на остальные случайные факторы приходится 2,9% изменчивости. Однако, этот вывод действителен только для рассматриваемого интервала значений X.
Этот результат истолковывается так: 97,1% изменчивости Y объясняется изменением фактора X, а на остальные случайные факторы приходится 2,9% изменчивости. Однако, этот вывод действителен только для рассматриваемого интервала значений X. точечную оценку для y получим путём подстановки
точечную оценку для y получим путём подстановки  в формулу (28):
в формулу (28):  Доверительный интервал для
Доверительный интервал для 




