Метод измерения
Пусть в баллоне первоначально было атмосферное давление P а. Если быстро повысить давление в баллоне и закрыть кран, то окончательная разность уровней в манометре h 1 установится не сразу (при быстром сжатии температура газа в баллоне повысится и пройдет некоторое время, пока температура воздуха в баллоне не сравняется, за счет теплопроводности, с температурой окружающего воздуха). При всех дальнейших наблюдениях надо мысленно выделить в сосуде некоторую массу воздуха объемом V и рассматривать изменения, происходящие только с этим количеством воздуха. Предположим, что происходящие с газом изменения изображены на графике, выражающем зависимость P от V (рис. 2.2).
Обозначим температуру окружающего воздуха Т о, а через Р 1 – давление газа внутри баллона. Это давление равно сумме атмосферного (барометрического) давления Р а и давления, определяемого по манометру Р ’, т. е. Р 1 = Р а + Р ’. Состояние газа характеризуемого параметрами Р 1, Т о, V 1, назовем первым состоянием газа. Если теперь быстро открыть кран, то воздух будет адиабатически расширяться, в результате чего давление внутри баллона достигнет атмосферного Р а; выделенная нами масса газа займет новый объем V 2, а температура станет ниже комнатной, т. е. газ охладится до температуры Т 2. Новое состояние газа на рис. 2.2 отмечено точкой 2 с параметрами Р о, Т 2, V 2. Если после открывания крана и выравнивания давления его снова закрыть, то воздух в баллоне, охладившийся при адиабатическом расширении, вновь нагреется до температуры окружающей среды Т о. Поскольку при этом нагревании объем воздуха V 2 не изменяется, то давление в баллоне несколько повысится и станет равным Р 2. О повышении давления воздуха в баллоне можно судить по повышению жидкости в левом колене манометра. Разность уровней при этом станет h 2. Новое состояние на графике изображается точкой 3 с параметрами Р 2, Т о, V 2. Таким образом, из состояния 1 в состояние 3 газ пришел, пройдя состояние 2 (сплошная линия). Из состояния 1 в состояние 3 газ мог прийти в результате изотермического расширения, так как в обоих состояниях температура газа одинакова (пунктирная линия). Итак, мы имеем три состояния газа, которые характеризуются следующими параметрами: 1 состояние – Т о, Р а + Р ’, V 1; 2 состояние – Р а, Т 2, V 2; 3 состояние – Т о, Р а + Р ’’, V 2. Рассматривая газ как идеальный, с помощью уравнений адиабатического (1.20) и изохорического процессов запишем выражения, связывающие параметры газов в трех состояниях. Адиабатический процесс (переход из состояния 1 в состояние 2):
Изохорический процесс (переход из состояния 2 в состояние 3):
Разделив уравнение (2.1) на (2.2), после преобразований получим
Прологарифмируем это выражение:
Так как по условию проведения опытов Учитывая, что ln (1+ x)» x, при x <<1
Выразив g из уравнения (2.4), получим формулу
Так как P’ соответствует установившемуся показанию манометра в состоянии 1 и измеряется высотой столба жидкости h 1, а P ’’ соответствуют показанию манометра в состоянии 3 и измеряется высотой h 2, то расчетная формула данного метода будет иметь вид
|


 . (2.1)
. (2.1) . (2.2)
. (2.2) .
.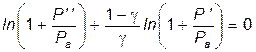 . (2.3)
. (2.3) и
и 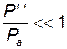 , то можно упростить выражение (2.3).
, то можно упростить выражение (2.3). (2.4)
(2.4)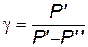 .
.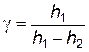 (2.5)
(2.5)


