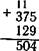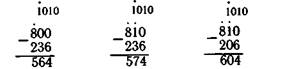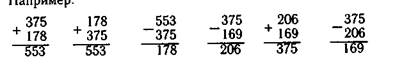Quot;-"• з •? к КПП
546 ~287 ~36Т 710 710 ~345 ~345 —^ту^- —тге- или Нередко при вычитании можно встретить и такую ошибку: вместо того чтобы «занять» единицу высшего разряда, раздробить ее, ученик начинает вычитать из большей цифры вычитаемого меньшую цифру соответствующего разряда уменьшаемого. Например:" 375 529 ^___ 8 ~145 373 424 При этом рассуждение проводится так: «Из 5 единиц 8 единиц вычесть нельзя, вычитаем из 8 единиц 5, 7 десятков и 3 сотни сносим, разность 373». Учитывая трудности изучения данной темы, необходимо повторить с учащимися сложение и вычитание с переходом через разряд в пределах 20 и 100, обратить внимание на решение примеров, в которых компонентом является нуль, или нуль получается в одном из разрядов суммы или __________,_______ :_____________ разности (17+3, 25+15, 36-6, 36—27), или нуль содержится в одном из разрядов уменьшаемого или вычитаемого (60—45, 75—40). I Тем учащимся, которые долгое время не усваивают запис! примеров в столбик, можно разрешить записывать их в разряди) сетку. При решении примеров на сложение и вычитание с переходе через разряд соблюдается следующая последовательность: 1) сложение и вычитание с переходом через разряд в одно разряде (единиц или десятков):
375 "146
Особого внимания заслуживает решение примеров вида 800— —236, 810—236, 810—206. Следует сопоставить сначала 1-й и 2-й, а потом 2-й и 3-й примеры, особенности их решения, объяснить, в чем их различие, почему получаются разные ответы.
2) сложение и вычитание с переходом через разряд в двуй 3) особые случаи сложения и вычитания, когда в сумме или в
4) вычитание трехзначных, двузначных и однозначных чисел из 1000: 1000-375, 1000-75, 1000-5. При объяснении решения примеров с переходом через разряд, учитывая, что умственно отсталые школьники при сложении забывают прибавлять то число, которое надо запомнить, можно разрешать надписывать это число над соответствующим разрядом. Например:
+ 375 118 ~493~ При вычитании же ставится точка над тем разрядом, из которого заняли единицу. Можно поставить и число 10, которое записывается над разрядом, к единицам которого этот десяток прибавляется.
При выполнении действий на сложение и вычитание в пределах 1000 решаются примеры с тремя компонентами без скобок и с круглыми скобками: 375+36+124; 379+(542-276); 910-375--264, 375+186-264, 1000-565+136. Решаются также примеры на нахождение неизвестных компонентов действий. Проверка выполняется двумя действиями.
Умножение и деление в пределах 1000 Умножение и деление так же, как сложение и вычитание, могут производиться как устными, так и письменными приемами вычислений, записываться в строчку и столбик. I. Устное умножение и деление в пределах 1000. 1. Умножение и деление круглых сотен. Умножение и деление круглых сотен основывается на знании учащимися нумерации, а также табличного умножения и деления. Поэтому, прежде чем знакомить учащихся с умножением и делением круглых сотен, необходимо повторить табличное умножение и деление, а также раздробление сотен в единицы и наоборот. Например: «Сколько содержит 1 сотня единиц? Сколько единиц в 5, 7, 10 сотнях? Сколько сотен составляют 300 единиц? 500 единиц?» И т. д. Объяснение умножения и деления должно сопро- вождаться операциями с наглядными пособиями и дидактичес|| материалом. Покажем объяснение умножения, а потом деления. Например, надо 200-2. Рассуждаем так: 200 — это 2 соТ| При делении 200:2 рассуждаем так: 200 — это 2 сотни. Воз! мем 2 сотни палочек. Если разделить их на две равные части, -т в каждой части получится по одной сотне, или по 100 единим Запишем: 2 сот.:2=1 сот. = 100, 200:2=100. Полезно сопоставим, умножение и деление единиц, десятков и сотен: ц итков). Делим 18 десятков на 3. Получим 6 десятков, или 60. щишем: 18 дес.:3=6 дес. =60, 180:3=60». Процесс деления;но показать и на палочках, и на брусках. Сначала учащиеся г. подробную запись, заменяя единицы десятками, затем запись _!ртывается. От учащихся требуется лишь устное объяснение. [яконец, свертывается и объяснение. Учащиеся записывают лишь т. Такое же объяснение проводится и при знакомстве с умножением и делением круглых десятков на однозначное число. Решети- подобных случаев сводится к внетабличному умножению и |и чению. Поэтому приведем лишь подробную запись решения:
3-3= 9 30-3= 90 300-3=900 8:4= 2 80:4= 20 800:4=200 120-4=? 12 дес. -4 дес.=48 дес.=480 120-4=480 480:4=? 48 дес.:4= 12 дес.= 120 480:4=120
Действия умножения и деления надо сопоставлять, проверяя каждое обратным действием: 400x2=800, 800:2=400. 2. Умножение и деление круглых десятков на однозначное число. а) Рассматриваются случаи умножения и деления круглых де б) Рассматриваются случаи, которые сводятся к внетабличному| Перед умножением и делением круглых десятков с учащимися необходимо повторить табличное и внетабличное умножение и деление (4-6, 24-2, 36:6, 36:3), а также определение общего количества десятков в числе («Сколько всего десятков в числе 120, 180, 360, 720?») и количества единиц в десятках («7 десятков. Сколько это единиц?»; «Сколько единиц з 2 десятках? 5 десятках? 10 десятках? 52 десятках?»). При объяснении проводятся следующие рассуждения: «60-3=? 60 — это 6 десятков, 6 дес.-3=18 дес. 18 десятков — это 180, значит, 60-3=180». Можно показать учащимся на брусках арифметического ящика, пучках палочек, связанных десятками, что результат будет тот же. Для этого учитель берет по 6 брусков 3 раза. Получает 18 брусков, или 18 десятков. Это число 180. При знакомстве с делением ход рассуждения аналогичен: «180:3=? Узнаем, сколько десятков содержится в числе 180 (18 200 123-3=?_________ 123 = 100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369 123=100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369 486:2 =?________ 486=400+80+6 400:2=200 80:2= 40 6:2= 3 200+40+3=243 100-3=300 20-3= 60 3-3= 9 300+60+9=369 4. Умножение 10 и 100, умножение на 10 и 100. В пределах 1000 рассматривается умножение однозначного двузначного числа на 10 и 100 и соответствующие случаи дел* ния: 8-100=800 8- 10= 80 80- 10=800
Умножение числа 10 учитель объясняет, опираясь на понятии умножения как сложения равных чисел. 10-3=10+10+10=30 10-3=30 10-5=10+10+10+10+10=50 10-5=50 Рассматривается еще несколько примеров. Сравниваются отве ты. Учащиеся убеждаются, что при умножении числа 10 на любой множитель к нему справа приписывается нуль. Затем решаются примеры на умножение однозначного числа ня 10. Решение примера 3x10=? также производится приемом заме ны умножения сложением одинаковых слагаемых: 3-10=3+3+3...+3=30 10 раз 1 Можно использовать и переместительный закон умножения: \ 10-3=30 3-10=30 Рассмотрев ряд таких примеров, сопоставив произведения и первый множитель, учащиеся приходят к выводу: чтобы умножить число на 10, нужно к первому множителю приписать справа один нуль. Это правило умножения числа на 10 распространяется и на умножение двузначных чисел (25x10=250). При умножении на 100 множитель 100 рассматривается как произведение двух чисел: 100=10* 10. Учащиеся практически знакомятся с использованием сочетательного закона умножения, хотя этот закон они не называют и не формулируют. Учитель объясняет: «Чтобы число умножить на 100, его нужно умножить сначала на 10,.. потом произведение умножить еще раз на 10, так как 100=10.10». Затем запись дается в строчку: 6-100=6-10 • 10=600. Решается также подробно еще несколько примеров. При реше-«и каждого примера учитель просит сравнивать произведение и!рвый множитель. Учащиеся самостоятельно приходят к выводу: •обы умножить число на 100, к нему нужно приписать справа а нуля. Умножение 100 на однозначное число выполняется путем ис- пьзования переместительного закона умножения: 100x5=? 5x100=500 5. Целение на 10 и 100. Деление на 10, как показывает опыт, лучше усваивается учащимися при сопоставлении с действием умножения. Деление на 10 рассматривается как деление по содержанию: 2-10=20, отсюда 20:10=2. 20:10=2 сопровождается вопросом: «Сколько раз в двух десятках содержится один десяток?» Как и в умножении, решается несколько примеров на деление на 10, сравниваются частное и делимое. Учащиеся убеждаются, [• что в частном получается делимое без одного нуля, и делают вывод: чтобы разделить число на 10, в нем надо отбросить нуль справа. Этот вывод распространяется и на деление круглых сотен и десятков на 10 (400:10=40, 250:10=25). Аналогично учащиеся знакомятся с делением на 100: 400:100=? 4-100=400 400:100=4 Деление на 100 можно объяснить и последовательным делением на 10 и еще раз на 10:
400:100=400:10:10=4 Деление на 10 и 100 учащиеся учатся производить как без остатка, так и с остатком: 40:10=4, 45:10=4 (ост. 5). Следует указать, что при делении числа на 10 (100) опредв ется, сколько всего десятков (сотен) содержится в нем. Учите, необходимо помнить о том, что умственно отсталые школьникь трудом дифференцируют сходные и противоположные понят|| Поэтому, когда ученики познакомились с правилами умножена деления числа на 10, 100, необходимо рассмотреть случаи, | которых эти правила используются одновременно, попросить щихся сравнить их, найти сходство и различие:
40: 10 400: 10 400:100 Необходимо также сравнить умножение на 10 и 100 с умнонв Закреплению действия способствует также кратное сравнение! чисел (во сколько раз одно число больше или меньше другого).; Например, даются такие задания: «Во сколько раз 2 меньше, чем/ 20, 200?»; «Во сколько раз 300 больше, чем 3, 10, 100?» Пример 300:3=100 можно прочитать так: «Число 300 больше, чем 3, в 100 раз». Или: «Число 3 меньше, чем 300, в 100 раз». «Какими действиями можно сравнить числа 400 и 10?» — спрашивает учитель. Ученики отвечают: «Сравнить эти числа можно действиями деления и вычитания: 400:10, 400—10». Учащиеся учатся самостоятельно ставить вопросы: «На сколько число 400 больше 10?»; «Во сколько раз 400 больше 10?» II. Письменное умножение и деление в пределах 1000.
|