ПОКАЗАТЕЛИ ВАРИАЦИИ В АНАЛИЗЕ ВЗАИМОСВЯЗЕЙ
Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации. Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение. Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Особое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств. Основными показателями, характеризующими вариацию, являются: размах, среднее линейное отклонение; дисперсия, среднее квадратическое отклонение, коэффициент вариации. 1. Размах вариации
Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:
где 3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:
4. Среднее квадратическое отклонение – корень квадратный из дисперсии:
В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (руб., тыс., млн и т.д.). 5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:
Для иллюстрации расчетов воспользуемся данными нижеприведенной таблицей 9.1: Таблица 9.1 Данные о продаже основных марок холодильников
Рассчитаем размах вариации.
Этот показатель служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных. Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака. Этого недостатка лишен другой показатель – дисперсия, рассчитываемая как средний квадрат отклонений значений признака от их средней величины. Между индивидуальными отклонениями от средней и колеблемостью признака существует прямая зависимость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и тем менее устойчив изучаемый показатель. Как и средняя величина, этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной. По приведенным выше данным определим средневзвешенную цену холодильника и рассчитаем дисперсию:
Следует отметить, что дисперсия еще не дает представления об однородности совокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рассчитан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, насколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. Рассчитаем среднее квадратическое отклонение:
Таким образом, цена каждой марки холодильника отклоняется от средней цены в среднем на 271,1 $. Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости какого-либо одного признака или для определения однородности совокупности рассчитывают относительные показатели. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.
Определим значение показателя вариации по вышеприведенным данным таблицы
Совокупность считается однородной, если V не превышает 33 %. Если Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33 % (для распределений, близких к нормальному). Следует отметить, что коэффициент вариации может быть более 100 %, что, в частности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине. Изучая вариацию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака. При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками: факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подверженным влиянию). Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индивидуальных значений признака, используют правило сложения дисперсий. Общая дисперсия представляет собой сумму средней из виутригрупповой и межгрупповой и дисперсий:
где
Общая дисперсия характеризует вариацию признака по всей совокупности как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.
где
Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.
где
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами, внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рассчитывается отдельно по каждой j-ой группе.
где
Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:
Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий: Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения:
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками. На следующем условном примере исследуем зависимость объема выполненных работ от формы собственности проектно-изыскательских организаций. Таблица 9.2 Выполнение работ проектно-изыскательскими организациями
1. Определим средний объем работ для предприятий двух форм собственности.
2. Определим средний объем работ для каждой формы собственности.
3. Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.
4. Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета. Таблица 9.3 Вспомогательная таблица
Средняя из внутригрупповых дисперсий
Межгрупповая дисперсия
На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий: 54,0+189,8=243,8. Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22 % [(54,0/243,8) ´ 100 %] зависит от фактора, положенного в основание группировки, т.е. от формы собственности, а на 78 % [(189,8/243,8) ´ 100 %)] – от прочих факторов. Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:
Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика. Контрольные задания 1. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:
Вычислить: а) размах вариации; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относительные показатели вариации возраста студентов. 2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.
|

 . (9.1)
. (9.1) – (для несгруппированных данных); (9.2)
– (для несгруппированных данных); (9.2) – (для вариационного ряда), (9.3)
– (для вариационного ряда), (9.3) – абсолютные значения отклонений отдельных вариантов xi от средней арифметической
– абсолютные значения отклонений отдельных вариантов xi от средней арифметической  ; fi – частота.
; fi – частота. (9.4)
(9.4) – (для несгруппированных данных); (9.5)
– (для несгруппированных данных); (9.5) – (для вариационного ряда). (9.6)
– (для вариационного ряда). (9.6) (9.7)
(9.7) $.
$. $;
$; .
. $.
$.
 (9.8)
(9.8) – общая дисперсия;
– общая дисперсия; – средняя из внутригрупповых дисперсий;
– средняя из внутригрупповых дисперсий; – межгрупповая дисперсия.
– межгрупповая дисперсия. (9.9)
(9.9) – отдельные значения признака;
– отдельные значения признака; – общая средняя варьирующего признака;
– общая средняя варьирующего признака; – вес варианта признака в общей совокупности.
– вес варианта признака в общей совокупности. , (9.10)
, (9.10) – средняя j -ой группы;
– средняя j -ой группы; – число единиц в j -ой группе
– число единиц в j -ой группе  .
. (9.11)
(9.11) – значение признака у отдельных элементов j -ой группы
– значение признака у отдельных элементов j -ой группы (9.12)
(9.12) . Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении общей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчленения общей совокупности.
. Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении общей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчленения общей совокупности. . (9.13)
. (9.13)
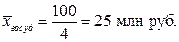

 ;
; ;
; ;
; .
. .
.



