Производство и оптимум производителя
Задачи
1. Производство стульев характеризуется функцией  .
. 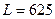 часов труда за неделю,
часов труда за неделю,  часов работы машин за неделю. Найдите недельный выпуск (
часов работы машин за неделю. Найдите недельный выпуск ( ). На сколько часов следует увеличить затраты труда (
). На сколько часов следует увеличить затраты труда ( ), чтобы выпуск не изменился (
), чтобы выпуск не изменился ( ), а количество работы машин сократилось на 1 час (
), а количество работы машин сократилось на 1 час ( )? Определите отдачу от масштаба.
)? Определите отдачу от масштаба.
2. Выпуск сливочного масла задан функцией 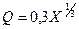 , где Q - объем выпуска масла,
, где Q - объем выпуска масла,  - расход молока. Определить прирост выпуска масла при увеличении расхода молока с
- расход молока. Определить прирост выпуска масла при увеличении расхода молока с  до
до 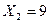 .
.
3. Определите предельную норму технологического замещения ( ), если производственная функция имеет вид
), если производственная функция имеет вид  , затраты труда равны 4, а капитала – 8.
, затраты труда равны 4, а капитала – 8.
4. При росте расходов труда на 4 единицы и сокращении расходов капитала на 3 единицы выпуск возрастает. А при росте расходов труда на 3 единицы и сокращении расходов капитала на 5 единиц выпуск сокращается. Определите предельную норму технологического замещения ( ).
).
5. При цене труда  и цене капитала
и цене капитала  издержки производства составляют
издержки производства составляют  . Запишите уравнение изокосты. Определите наклон изокосты к оси OL и OK. Как изменится наклон изокосты, если обе цены возрастут на 15 %?
. Запишите уравнение изокосты. Определите наклон изокосты к оси OL и OK. Как изменится наклон изокосты, если обе цены возрастут на 15 %?
6. Определить эластичность замены труда капиталом ( ) для следующих производственных функций:
) для следующих производственных функций:  ;
;  ;
; 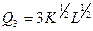 ;
;  .
.
7. Технология разгрузки вагонов описана производственной функцией  , где
, где  - количество разгруженных вагонов;
- количество разгруженных вагонов;  - труд,
- труд,  - оборудование.
- оборудование.  руб. в неделю, а аренда одной единицы оборудования
руб. в неделю, а аренда одной единицы оборудования  руб. в неделю. Какое количество труда и оборудования необходимо, чтобы разгрузить 160 вагонов за неделю? Известно, что издержки фирмы по разгрузке
руб. в неделю. Какое количество труда и оборудования необходимо, чтобы разгрузить 160 вагонов за неделю? Известно, что издержки фирмы по разгрузке  руб. в неделю. Какое количество вагонов может быть разгружено фирмой, минимизирующей издержки? Если аренда одной единицы оборудования стала в 2 раза дешевле, сколько теперь надо труда и оборудования, чтобы разгрузить 160 вагонов за неделю?
руб. в неделю. Какое количество вагонов может быть разгружено фирмой, минимизирующей издержки? Если аренда одной единицы оборудования стала в 2 раза дешевле, сколько теперь надо труда и оборудования, чтобы разгрузить 160 вагонов за неделю?
Издержки фирмы и ее равновесие в условиях
совершенной конкуренции
Задачи
1. При выпуске  валовые переменные издержки составляют
валовые переменные издержки составляют  и валовые постоянные -
и валовые постоянные -  , предельные издержки одинаковы для каждой единицы продукции. Необходимо найти средние валовые, средние переменные и средние постоянные издержки при выпуске
, предельные издержки одинаковы для каждой единицы продукции. Необходимо найти средние валовые, средние переменные и средние постоянные издержки при выпуске  .
.
2. При производстве  валовые издержки фирмы составляют
валовые издержки фирмы составляют 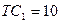 , а при выпуске
, а при выпуске  -
-  . Предельные издержки фирмы неизменны на каждую единицу продукции. Найдите валовые постоянные и переменные издержки фирмы при выпуске
. Предельные издержки фирмы неизменны на каждую единицу продукции. Найдите валовые постоянные и переменные издержки фирмы при выпуске  .
.
3. Издержки производства первого автомобиля составляют  , при сборке каждого последующего автомобиля издержки возрастают на 0,1. Запишите функции валовых издержек (
, при сборке каждого последующего автомобиля издержки возрастают на 0,1. Запишите функции валовых издержек ( ) и предельных издержек (
) и предельных издержек ( ). Найдите дополнительные издержки, которые потребуются для сборки сотого автомобиля (
). Найдите дополнительные издержки, которые потребуются для сборки сотого автомобиля ( ).
).
4. Издержки производства первого килограмма меда составляют  , при росте производства меда на 1 кг издержки возрастают на
, при росте производства меда на 1 кг издержки возрастают на  . Определите предельные издержки (
. Определите предельные издержки ( ) при производстве
) при производстве  кг меда и при производстве
кг меда и при производстве  кг меда.
кг меда.
5. Постоянные издержки производства  , издержки производства первого изделия составляют
, издержки производства первого изделия составляют  , а издержки производства дополнительной единицы продукции возрастают на 2. Запишите функцию валовых издержек фирмы (
, а издержки производства дополнительной единицы продукции возрастают на 2. Запишите функцию валовых издержек фирмы ( ).
).
Модели олигополии
Задачи
1. На рынке дуополии функционируют 2 фирмы с общими издержками  . Выпуск первой фирмы задан функцией
. Выпуск первой фирмы задан функцией  , выпуск второй фирмы описывается функцией
, выпуск второй фирмы описывается функцией  . Найдите равновесный выпуск и цену каждой из фирм, а также их прибыль в случае минимизации издержек. Определите степень монопольной власти каждой из фирм.
. Найдите равновесный выпуск и цену каждой из фирм, а также их прибыль в случае минимизации издержек. Определите степень монопольной власти каждой из фирм.
2. В отрасли действуют две фирмы, предельные издержки которых одинаковы и равны нулю. Спрос на продукцию отрасли равен  , где
, где 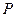 - цена (руб. за шт.),
- цена (руб. за шт.),  - объем спроса (тыс. шт.). Определите: 1) Каким образом фирмы поделят рынок между собой в условиях равновесия Курно? Какой при этом будет цена равновесия? 2) Если фирмы объединяться в картель, какое количество товаров они выпустят и по какой цене продадут? 3) Если бы в отрасли существовала совершенная конкуренция, чему бы была равна цена и какой объем производства был бы характерен для нее?
- объем спроса (тыс. шт.). Определите: 1) Каким образом фирмы поделят рынок между собой в условиях равновесия Курно? Какой при этом будет цена равновесия? 2) Если фирмы объединяться в картель, какое количество товаров они выпустят и по какой цене продадут? 3) Если бы в отрасли существовала совершенная конкуренция, чему бы была равна цена и какой объем производства был бы характерен для нее?
3. Исследование рынка, находящегося в условиях дуополии, установило, что функции реагирования каждой фирмы имеют следующий вид: 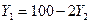 ;
;  , где
, где  и
и 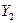 характеризуют объемы производства соответственно первой и второй фирмы. Изобразите функции реагирования графически и вычислите пропорции раздела рынка между ними.
характеризуют объемы производства соответственно первой и второй фирмы. Изобразите функции реагирования графически и вычислите пропорции раздела рынка между ними.
4. На рынке действуют две фирмы, общие издержки первой составляют  , а второй соответственно
, а второй соответственно  . Отраслевой спрос равен
. Отраслевой спрос равен  . Определите равновесные параметры и прибыль каждой фирмы в соответствии с моделью Штакельберга. Как изменятся равновесные параметры фирм, если будет действовать модель Курно?
. Определите равновесные параметры и прибыль каждой фирмы в соответствии с моделью Штакельберга. Как изменятся равновесные параметры фирм, если будет действовать модель Курно?
Модель монополии и ее социально-экономические последствия
Задачи
1. Необходимо определить степень монопольной власти фирмы: 1) если ценовая эластичность спроса составляет  ,
, 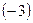 ; 2) если рыночная цена составляет 10, а предельный доход фирмы равен 5. 3) Чему равен индекс Лернера для фирмы совершенного конкурента и для фирмы-монополиста?
; 2) если рыночная цена составляет 10, а предельный доход фирмы равен 5. 3) Чему равен индекс Лернера для фирмы совершенного конкурента и для фирмы-монополиста?
2. Валовые издержки фирмы-монополиста заданы функцией  . Спрос монополиста
. Спрос монополиста  . Найти равновесные значения выпуска и цены монополиста, если 1) фирма максимизирует валовой доход (определите соответствующую величину дохода); 2) фирма максимизирует прибыль (определите соответствующую величину).
. Найти равновесные значения выпуска и цены монополиста, если 1) фирма максимизирует валовой доход (определите соответствующую величину дохода); 2) фирма максимизирует прибыль (определите соответствующую величину).
Изобразите графически следующие случаи: 1) фирма-монополист несет убытки, но не закрывается; 2) различие монополиста и совершенного конкурента при введении потолка цен.
3. Квашеная капуста производится в условиях совершенной конкуренции. Функция спроса на квашеную капусту имеет вид  , где
, где  - количество капусты в день (измеряемое ведрами), а
- количество капусты в день (измеряемое ведрами), а 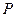 - цена за ведро капусты. Предложение квашеной капусты представлено следующей функцией:
- цена за ведро капусты. Предложение квашеной капусты представлено следующей функцией:  . Найдите равновесные значения объема и цены капусты. Каковы размеры избытка производителя и потребителя? Если предположить, что выпуск вынужденно ограничен 300 ведрами в день, то каковы будут совокупные потери избытка потребителей и избытка производителей? Дайте графическую иллюстрацию.
. Найдите равновесные значения объема и цены капусты. Каковы размеры избытка производителя и потребителя? Если предположить, что выпуск вынужденно ограничен 300 ведрами в день, то каковы будут совокупные потери избытка потребителей и избытка производителей? Дайте графическую иллюстрацию.
4. Внутренний спрос на продукцию фирмы-монополиста задан функцией  , его общие издержки -
, его общие издержки -  . На внешнем рынке можно продать любое количество продукции по цене 60 у.е. Определите цену внутреннего рынка, объем продаж на внутреннем и внешнем рынках и размер прибыли, максимизирующей прибыль фирмы. (
. На внешнем рынке можно продать любое количество продукции по цене 60 у.е. Определите цену внутреннего рынка, объем продаж на внутреннем и внешнем рынках и размер прибыли, максимизирующей прибыль фирмы. (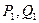 - мировые значения цены и объема выпуска;
- мировые значения цены и объема выпуска; 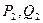 - отечественные значения цены и объема выпуска).
- отечественные значения цены и объема выпуска).
Регулирование деятельности
монополии с помощью налогообложения
1. Кривая спроса монополиста, производящего продукт 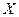 , имеет вид
, имеет вид  , где
, где 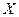 - выпуск в тыс. шт.,
- выпуск в тыс. шт., 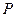 - цена продукта в рублях. Предельные издержки неизменны и равны 10 руб. 1) Монополист облагается потоварным налогом
- цена продукта в рублях. Предельные издержки неизменны и равны 10 руб. 1) Монополист облагается потоварным налогом  руб. Подсчитайте прибыль монополиста и сравните ее с прибылью в отсутствие налога. 2) Какова будет прибыль монополиста при ставке налога в 20 руб.? в 30 руб.? 3) Покажите с помощью графической иллюстрации, сохраняется ли убывание прибыли монополиста с ростом ставки потоварного налога в случае стандартных (U-образных) кривых издержек. 4) Пусть теперь регулирование монополиста осуществляется не с помощью налога, а путем установления максимальной цены на его продукцию на уровне 100 руб. за единицу. Каковы будут выпуск и прибыль монополиста в этом случае? В случае максимальной цены в 110 руб.? При какой максимальной цене монополист будет производить эффективный объем выпуска? Приведите графическую иллюстрацию решения.
руб. Подсчитайте прибыль монополиста и сравните ее с прибылью в отсутствие налога. 2) Какова будет прибыль монополиста при ставке налога в 20 руб.? в 30 руб.? 3) Покажите с помощью графической иллюстрации, сохраняется ли убывание прибыли монополиста с ростом ставки потоварного налога в случае стандартных (U-образных) кривых издержек. 4) Пусть теперь регулирование монополиста осуществляется не с помощью налога, а путем установления максимальной цены на его продукцию на уровне 100 руб. за единицу. Каковы будут выпуск и прибыль монополиста в этом случае? В случае максимальной цены в 110 руб.? При какой максимальной цене монополист будет производить эффективный объем выпуска? Приведите графическую иллюстрацию решения.
Раздел 2. Моделирование макроэкономических процессов
Тема 4. Модели общего экономического равновесия.
Модель Л.Вальраса
Задачи
1. Определите цены общего равновесия в хозяйстве, состоящем из двух отраслей со следующими функциями спроса и предложения:  ,
,  и
и  ,
,  . Каково будет соотношение между спросом и предложением в каждой отрасли, если
. Каково будет соотношение между спросом и предложением в каждой отрасли, если  ,
, 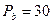 ?
?
Модель 
1. Агрегированная производственная функция характеризуется формулой  . Функция инвестиций имеет вид:
. Функция инвестиций имеет вид:  . Функция сбережений
. Функция сбережений 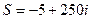 . Номинальное количество денег в обращении
. Номинальное количество денег в обращении  . Скорость обращения денег
. Скорость обращения денег  . Реальная ставка заработной платы в условиях полной занятости
. Реальная ставка заработной платы в условиях полной занятости  . Определите: 1) равновесный уровень цен; 2) равновесное значение процентной ставки; 3) реальный объем национального производства в условиях общего макроэкономического равновесия; 4) равновесный объем занятости.
. Определите: 1) равновесный уровень цен; 2) равновесное значение процентной ставки; 3) реальный объем национального производства в условиях общего макроэкономического равновесия; 4) равновесный объем занятости.
Модель  и возможные
и возможные
направления экономической политики
1. Пусть национальная экономика характеризуется следующими показателями: 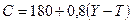 ,
,  ,
,  ,
,  .
.
В рамках модели кейнсианского креста:
а. Определите функцию планируемых расходов и нарисуйте ее график.
б. Вычислите равновесный уровень дохода.
в. Вычислите уровень незапланированных запасов, когда фактический выпуск составляет 3000.
2. В условиях данных задачи 2 рассмотрите следующие три случая: 1) государственные расходы возросли до 260; 2) при исходной величине государственных расходов налоги возросли до 160; 3) произошло одновременное увеличение государственных расходов и налогов на 10 ед.
Для каждого из случаев определите:
а. Что произойдет с графиком планируемых расходов?
б. В каком направлении и на какую величину изменятся равновесные уровни дохода, потребления и бюджетного дефицита?
3. Пусть в рамках модели кейнсианского креста экономика описывается следующим образом:  ,
,  ,
,  ,
,  .
.
а. Определите предельную склонность к потреблению.
б. Определите функции потребления и планируемых расходов и постройте их графики.
в. Вычислите равновесный уровень дохода. Чему равен бюджетный избыток при равновесном уровне дохода?
г. Пусть  . Найдите равновесный уровень дохода и, используя не формулу, а определение, вычислите мультипликатор государственных расходов.
. Найдите равновесный уровень дохода и, используя не формулу, а определение, вычислите мультипликатор государственных расходов.
4. Пусть экономика описывается следующим образом:  ,
,  ,
, 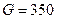 ,
,  ,
,  ,
,  ,
,  .
.
а. Выпишите уравнение кривой 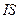 .
.
б. Выпишите уравнение кривой  .
.
в. Вычислите наклоны этих кривых.
г. Найдите равновесные уровни реального дохода, ставки процента, планируемых инвестиций и потребления.
д. Вычислите бюджетный избыток при равновесном уровне дохода.
5. Для линейного варианта модели  определите графически, как изменятся
определите графически, как изменятся 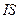 и
и  , если:
, если:
а. Возрастает чувствительность инвестиций к ставке процента?
б. Возрастает ставка налога?
в. Номинальное предложение денег неизменно, а уровень цен растет?
г. Возрастает чувствительность спроса на деньги к ставке процента?
д. Возрастает чувствительность спроса на деньги к доходу?
6. В рамках линейного варианта модели  определить алгебраически, объяснить экономически и дать графическую интерпретацию результатов проведения ограничительной фискальной и кредитно-денежной политик в краткосрочном и долгосрочном периодах, предполагая, что первоначально экономика находилась в состоянии краткосрочного равновесия, совпадающего с долгосрочным.
определить алгебраически, объяснить экономически и дать графическую интерпретацию результатов проведения ограничительной фискальной и кредитно-денежной политик в краткосрочном и долгосрочном периодах, предполагая, что первоначально экономика находилась в состоянии краткосрочного равновесия, совпадающего с долгосрочным.

 .
. 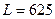 часов труда за неделю,
часов труда за неделю,  часов работы машин за неделю. Найдите недельный выпуск (
часов работы машин за неделю. Найдите недельный выпуск ( ). На сколько часов следует увеличить затраты труда (
). На сколько часов следует увеличить затраты труда ( ), чтобы выпуск не изменился (
), чтобы выпуск не изменился ( ), а количество работы машин сократилось на 1 час (
), а количество работы машин сократилось на 1 час ( )? Определите отдачу от масштаба.
)? Определите отдачу от масштаба.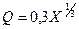 , где Q - объем выпуска масла,
, где Q - объем выпуска масла,  - расход молока. Определить прирост выпуска масла при увеличении расхода молока с
- расход молока. Определить прирост выпуска масла при увеличении расхода молока с  до
до 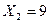 .
. ), если производственная функция имеет вид
), если производственная функция имеет вид  , затраты труда равны 4, а капитала – 8.
, затраты труда равны 4, а капитала – 8. и цене капитала
и цене капитала  издержки производства составляют
издержки производства составляют  . Запишите уравнение изокосты. Определите наклон изокосты к оси OL и OK. Как изменится наклон изокосты, если обе цены возрастут на 15 %?
. Запишите уравнение изокосты. Определите наклон изокосты к оси OL и OK. Как изменится наклон изокосты, если обе цены возрастут на 15 %? ) для следующих производственных функций:
) для следующих производственных функций:  ;
;  ;
; 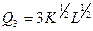 ;
;  .
. , где
, где  - труд,
- труд,  - оборудование.
- оборудование.  руб. в неделю, а аренда одной единицы оборудования
руб. в неделю, а аренда одной единицы оборудования  руб. в неделю. Какое количество труда и оборудования необходимо, чтобы разгрузить 160 вагонов за неделю? Известно, что издержки фирмы по разгрузке
руб. в неделю. Какое количество труда и оборудования необходимо, чтобы разгрузить 160 вагонов за неделю? Известно, что издержки фирмы по разгрузке  руб. в неделю. Какое количество вагонов может быть разгружено фирмой, минимизирующей издержки? Если аренда одной единицы оборудования стала в 2 раза дешевле, сколько теперь надо труда и оборудования, чтобы разгрузить 160 вагонов за неделю?
руб. в неделю. Какое количество вагонов может быть разгружено фирмой, минимизирующей издержки? Если аренда одной единицы оборудования стала в 2 раза дешевле, сколько теперь надо труда и оборудования, чтобы разгрузить 160 вагонов за неделю? валовые переменные издержки составляют
валовые переменные издержки составляют  и валовые постоянные -
и валовые постоянные -  , предельные издержки одинаковы для каждой единицы продукции. Необходимо найти средние валовые, средние переменные и средние постоянные издержки при выпуске
, предельные издержки одинаковы для каждой единицы продукции. Необходимо найти средние валовые, средние переменные и средние постоянные издержки при выпуске  .
. валовые издержки фирмы составляют
валовые издержки фирмы составляют 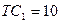 , а при выпуске
, а при выпуске  -
-  . Предельные издержки фирмы неизменны на каждую единицу продукции. Найдите валовые постоянные и переменные издержки фирмы при выпуске
. Предельные издержки фирмы неизменны на каждую единицу продукции. Найдите валовые постоянные и переменные издержки фирмы при выпуске  .
. , при сборке каждого последующего автомобиля издержки возрастают на 0,1. Запишите функции валовых издержек (
, при сборке каждого последующего автомобиля издержки возрастают на 0,1. Запишите функции валовых издержек ( ) и предельных издержек (
) и предельных издержек ( ). Найдите дополнительные издержки, которые потребуются для сборки сотого автомобиля (
). Найдите дополнительные издержки, которые потребуются для сборки сотого автомобиля ( ).
). , при росте производства меда на 1 кг издержки возрастают на
, при росте производства меда на 1 кг издержки возрастают на  . Определите предельные издержки (
. Определите предельные издержки ( кг меда и при производстве
кг меда и при производстве  кг меда.
кг меда. , издержки производства первого изделия составляют
, издержки производства первого изделия составляют  , а издержки производства дополнительной единицы продукции возрастают на 2. Запишите функцию валовых издержек фирмы (
, а издержки производства дополнительной единицы продукции возрастают на 2. Запишите функцию валовых издержек фирмы ( . Выпуск первой фирмы задан функцией
. Выпуск первой фирмы задан функцией  , выпуск второй фирмы описывается функцией
, выпуск второй фирмы описывается функцией  . Найдите равновесный выпуск и цену каждой из фирм, а также их прибыль в случае минимизации издержек. Определите степень монопольной власти каждой из фирм.
. Найдите равновесный выпуск и цену каждой из фирм, а также их прибыль в случае минимизации издержек. Определите степень монопольной власти каждой из фирм. , где
, где 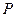 - цена (руб. за шт.),
- цена (руб. за шт.), 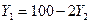 ;
;  , где
, где  и
и 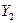 характеризуют объемы производства соответственно первой и второй фирмы. Изобразите функции реагирования графически и вычислите пропорции раздела рынка между ними.
характеризуют объемы производства соответственно первой и второй фирмы. Изобразите функции реагирования графически и вычислите пропорции раздела рынка между ними. , а второй соответственно
, а второй соответственно  . Отраслевой спрос равен
. Отраслевой спрос равен  . Определите равновесные параметры и прибыль каждой фирмы в соответствии с моделью Штакельберга. Как изменятся равновесные параметры фирм, если будет действовать модель Курно?
. Определите равновесные параметры и прибыль каждой фирмы в соответствии с моделью Штакельберга. Как изменятся равновесные параметры фирм, если будет действовать модель Курно? ,
, 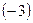 ; 2) если рыночная цена составляет 10, а предельный доход фирмы равен 5. 3) Чему равен индекс Лернера для фирмы совершенного конкурента и для фирмы-монополиста?
; 2) если рыночная цена составляет 10, а предельный доход фирмы равен 5. 3) Чему равен индекс Лернера для фирмы совершенного конкурента и для фирмы-монополиста? . Спрос монополиста
. Спрос монополиста  . Найти равновесные значения выпуска и цены монополиста, если 1) фирма максимизирует валовой доход (определите соответствующую величину дохода); 2) фирма максимизирует прибыль (определите соответствующую величину).
. Найти равновесные значения выпуска и цены монополиста, если 1) фирма максимизирует валовой доход (определите соответствующую величину дохода); 2) фирма максимизирует прибыль (определите соответствующую величину). , где
, где  . Найдите равновесные значения объема и цены капусты. Каковы размеры избытка производителя и потребителя? Если предположить, что выпуск вынужденно ограничен 300 ведрами в день, то каковы будут совокупные потери избытка потребителей и избытка производителей? Дайте графическую иллюстрацию.
. Найдите равновесные значения объема и цены капусты. Каковы размеры избытка производителя и потребителя? Если предположить, что выпуск вынужденно ограничен 300 ведрами в день, то каковы будут совокупные потери избытка потребителей и избытка производителей? Дайте графическую иллюстрацию. , его общие издержки -
, его общие издержки -  . На внешнем рынке можно продать любое количество продукции по цене 60 у.е. Определите цену внутреннего рынка, объем продаж на внутреннем и внешнем рынках и размер прибыли, максимизирующей прибыль фирмы. (
. На внешнем рынке можно продать любое количество продукции по цене 60 у.е. Определите цену внутреннего рынка, объем продаж на внутреннем и внешнем рынках и размер прибыли, максимизирующей прибыль фирмы. (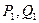 - мировые значения цены и объема выпуска;
- мировые значения цены и объема выпуска; 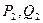 - отечественные значения цены и объема выпуска).
- отечественные значения цены и объема выпуска).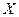 , имеет вид
, имеет вид  , где
, где  руб. Подсчитайте прибыль монополиста и сравните ее с прибылью в отсутствие налога. 2) Какова будет прибыль монополиста при ставке налога в 20 руб.? в 30 руб.? 3) Покажите с помощью графической иллюстрации, сохраняется ли убывание прибыли монополиста с ростом ставки потоварного налога в случае стандартных (U-образных) кривых издержек. 4) Пусть теперь регулирование монополиста осуществляется не с помощью налога, а путем установления максимальной цены на его продукцию на уровне 100 руб. за единицу. Каковы будут выпуск и прибыль монополиста в этом случае? В случае максимальной цены в 110 руб.? При какой максимальной цене монополист будет производить эффективный объем выпуска? Приведите графическую иллюстрацию решения.
руб. Подсчитайте прибыль монополиста и сравните ее с прибылью в отсутствие налога. 2) Какова будет прибыль монополиста при ставке налога в 20 руб.? в 30 руб.? 3) Покажите с помощью графической иллюстрации, сохраняется ли убывание прибыли монополиста с ростом ставки потоварного налога в случае стандартных (U-образных) кривых издержек. 4) Пусть теперь регулирование монополиста осуществляется не с помощью налога, а путем установления максимальной цены на его продукцию на уровне 100 руб. за единицу. Каковы будут выпуск и прибыль монополиста в этом случае? В случае максимальной цены в 110 руб.? При какой максимальной цене монополист будет производить эффективный объем выпуска? Приведите графическую иллюстрацию решения. ,
,  и
и  ,
,  . Каково будет соотношение между спросом и предложением в каждой отрасли, если
. Каково будет соотношение между спросом и предложением в каждой отрасли, если  ,
, 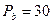 ?
?
 . Функция инвестиций имеет вид:
. Функция инвестиций имеет вид:  . Функция сбережений
. Функция сбережений 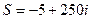 . Номинальное количество денег в обращении
. Номинальное количество денег в обращении  . Скорость обращения денег
. Скорость обращения денег  . Реальная ставка заработной платы в условиях полной занятости
. Реальная ставка заработной платы в условиях полной занятости  . Определите: 1) равновесный уровень цен; 2) равновесное значение процентной ставки; 3) реальный объем национального производства в условиях общего макроэкономического равновесия; 4) равновесный объем занятости.
. Определите: 1) равновесный уровень цен; 2) равновесное значение процентной ставки; 3) реальный объем национального производства в условиях общего макроэкономического равновесия; 4) равновесный объем занятости. и возможные
и возможные 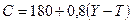 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. . Найдите равновесный уровень дохода и, используя не формулу, а определение, вычислите мультипликатор государственных расходов.
. Найдите равновесный уровень дохода и, используя не формулу, а определение, вычислите мультипликатор государственных расходов. ,
,  ,
, 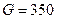 ,
,  ,
,  ,
,  ,
,  .
.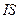 .
. .
.


