общий партнер – а general partner
неограниченная ответственность – unlimited liability
страхование – insurance
вести дело – to carry out a business
недвижимость – real estate
прибыль – profit
биржевое маклерство – stockbrokerage
добыча нефти – oil prospecting
часто получают льготы по налогообложению -often get tax benefits
Задание 9. Ответьте на вопросы к тексту
1. What is the difference between a general partnership and a limited partnership? -The difference is the following.When the owners of the partnership have unlimited liability they are called general partners. If partners have limited liability they are “limited partners”.
2. Is there a difference between a silent partner and a secret partner? – Yes, there is. A silent partner is known to the public as a member of the firm but without authority in management. The secret partner takes part in management but is not known to the public.
3. What are the advantages and disadvantages of a partnership? – Partnerships have more advantages than sole proprietorships if one needs a big capital or diversified management. Like sole proprietorships they are easy to form and often get tax benefits from the government. Partnerships have certain disadvantages too. One of them is unlimited liability. It means that each partner is responsible for all debts and is legally responsible for the whole business. Another disadvantage is that partners may disagree with each other.
Контрольная работа по информатике
| 1.
| Создайте рабочую книгу Excel c именем Фамилия_Шифр_КР-Excel.xls. В свойствах файла в поле Автор укажите свою фамилию, в поле Ключевые слова – Ваш шифр и дату создания Вами файла (день, месяц, год).
|
|
| 2.
| Переименуйте первый лист рабочей книги, назвав его Шифр_Вариант-2.
|
|
| 3.
| Для ячеек K1 и L1 установите белый цвет текста.
|
|
| 4.
| Объедините ячейки В1-H1 и в полученную ячейку введите свою фамилию и инициалы, применив следующий формат: размер символов 12 пт, шрифт – полужирный, изображение символов – по правому краю ячейки красным цветом на желтом фоне. Установите высоту второй строки – 28,14.
|
|
| 5.
| Вычислите коэффициенты α и β:
α = <Три первые цифры вашего шифра (номер студенческого билета)> + <№ варианта * 10>
β = <Две последние цифры вашего шифра> + 1
Введите в ячейку Zβ вашу фамилию, а в ячейку Xα ваше имя.
Например:
студент Иванов Иван, шифр 13056.
Вариант 5+6=11
α =130+11*10=240
β =56+1=57
Таким образом, значение ячейки Z57 будет «Иванов», а ячейки X240 – «Иван».
|
|
| 6.
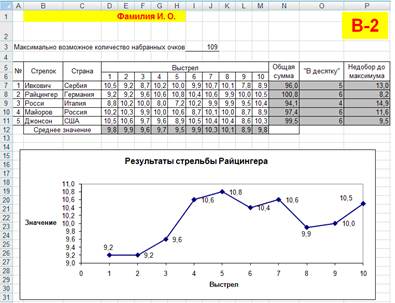
| 6.1. Задача: на Олимпийский Играх в финал по стрельбе из пневматической винтовки вышли 5 спортсменов. Каждый спортсмен сделал по 10 выстрелов. Определите: общую сумму очков, набранных каждым стрелком, за все выстрелы; среднее значение очков, набранных всеми стрелками, за выстрел; сколько баллов недобрал каждый стрелок до максимально возможного числа.
По исходным данным рис. 1 в соответствии с представленным на нем образцом создайте таблицу, выполните расчеты и постройте диаграмму, отражающую результаты стрельбы спортсмена из Германии (тип диаграммы – точечная, вид – точечная диаграмма, на которой значения соединены отрезками).
Перед вводом исходных данных в ячейки D7:М11 установите проверку данных, задав условие, что вводимое значение не должно быть больше 10,9.
Данные в ячейки, к которым применена заливка серым цветом, определите с помощью формул и функций.
При расчете количества баллов, которые недобрал спортсмен до максимально возможного числа, следует использовать абсолютную ссылку на ячейку J3!
6.2. В ячейках О7:О11 с помощью встроенных функций для каждого спортсмена определите количество выстрелов «в десятку».
6.3. Отфильтруйте созданную таблицу с учетом условия, что общая сумма набранных очков больше 96,5.
|
|
|
|
|
|
|
| Рис. 1
|
|
| 7.
| В ячейке K1 установите относительную ссылку (формулу, а не гиперссылку) на ячейку Zβ, а в ячейке L1 – на Xα.
|
| 8.
| В верхнем колонтитуле укажите свои Ф.И.О. и индивидуальный шифр, а также дату выполнения контрольной работы. Например: Иванов И.И. 13056 27.02.2010
|
| 9.
| Переименуйте второй лист рабочей книги, назвав его Фамилия _ Матрицы.
|
| 10.
| Введите исходную матрицу и выведите транспонированную к ней по образцу рис. 2.
|
|
|
 Рис. 2.
Рис. 2.
|
| 11.
| Переименуйте третий лист рабочей книги, назвав его Корень уравнения.
|
| 12.
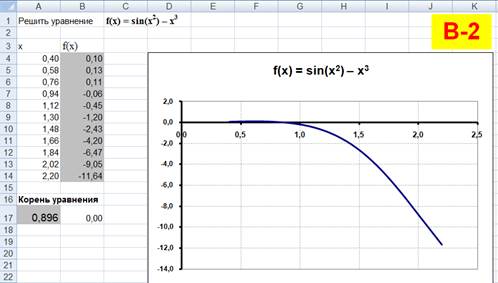
| По образцу рис. 3 постройте график функции f(x) = sin(x2) – x3 по 11-ти равноотстоящим точкам на отрезке [0,4; 2,2]. С помощью режима Подбор параметра найдите корень уравнения f(x)=0 при начальном приближении х=1 (о твет: х=0,8963). Скопируйте окно «Подбор параметра» с заданными Вами настройками и представьте его справа от диаграммы.
Значения аргумента х необходимо ввести с помощью режима автозаполнения ячеек!
|
|
|
|
|
| Рис. 3.
|
| 13.
| Создайте новый лист рабочей книги и назовите его СЛАУ.
(СЛАУ – система линейных алгебраических уравнений)
|
| 14.
| С помощью режима Поиск решения решите СЛАУ, представленную на рис. 4 (ответы: x=0,4692; y=0,8228; z=1,6528). Скопируйте окно «Поиск решения» с заданными Вами настройками и представьте его на любом свободном месте листа.
|
|
| 
|
|
| Рис. 4.
|
| 15.
| Из файла _ Итоги.xls скопируйте в конец рабочей книги с Вашей контрольной работой лист с именем, соответствующим номеру Вашего варианта, и выполните на созданном листе указанные на нем задания.
|


 Рис. 2.
Рис. 2.





