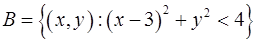О.А. Кадысева
Цены зависят от индивидуальных желаний, и обговариваются.
Услуги по полиграфии. От 01.01.11
Цены зависят от тиража.
МЕТОДИЧНА РОЗРОБКА Для проведення практичного заняття № 1 Тема № 1. Елементи теорії множин і відношень Множини і операції над ними
ПЛАН ПРОВЕДЕННЯ ЗАНЯТТЯ ТА РОЗРАХУНОК ЧАСУ
Вступ. Перевірити наявність студентів на занятті 5 хвилин
Навчальні питання: 1. Повторення основних положень лекції:…………………….10 хвилин 2. Розв’язування задач……………………..…………………….65 хвилин 3. Домашне завдання………………….………………………….5 хвилин Заключення 5 хвилин ЛІТЕРАТУРА: 1. Бардачов Ю.М. та ін. Дискретна математика. – К.: Вища школа, 2002. – 287 с. 2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2004. – 416 с. НАВЧАЛЬНІ МАТЕРІАЛИ 1. Повторення основних теоретичних положень: 1. Зміст та задачі дискретної математики. 2. Поняття множини. Способи завдання множини. 3. Відношення між множинами. 4. Геометричне зображення множин. 5. Основні операції над множинами: об’єднання, переріз, різниця, доповнення. 6. Властивості операцій над множинами. 7. Декартовий добуток множин.
2. Розв’язування задач: Завдання 1. Нехай 1)
Розв’язання: Побудуємо схематично дані множини:
внутрішня частина квадрату, утвореного перерізом прямих
За означеннями основних операцій над множинами будемо мати: 1)
2)
3)
4) Різниця множин
5) Доповнення до множини
6)
7)
Завдання 2. Довести справедливість співвідношень між множинами, використовуючи а) закони алгебри множин; б) діаграми Ейлера-Венна. Доведення. а) Використовуючи закони алгебри множин, маємо:
б) За допомогою діаграм Ейлера-Венна. Намалюємо діаграми окремо для лівої і правої частини рівності:
Оскільки заштриховані області на діаграмах збігаються, то рівність доведено.
Завдання 3. Знайти і зобразити в ПДСК множину
Розв’язання: За означенням декартового добутку
Зобразимо множину
Таким чином, декартовий добуток Самостійна робота за індивідуальними варіантами (зразок) Нехай 1)
Завдання 1. Нехай 1)
О.А. Кадысева
|

 – множина точок площини, на якій задана прямокутна декартова система координат. Знайти та зобразити на площині множини:
– множина точок площини, на якій задана прямокутна декартова система координат. Знайти та зобразити на площині множини: ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  , якщо
, якщо

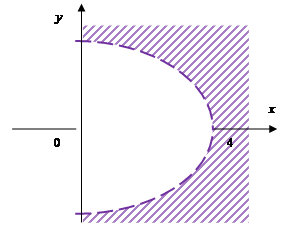
 Множина
Множина  – внутрішня частина параболи
– внутрішня частина параболи  з вершиною у точці
з вершиною у точці  :
: Множина
Множина 
 Об’єднання множин
Об’єднання множин 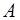 і
і  :
: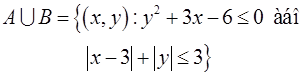
 Переріз множин
Переріз множин 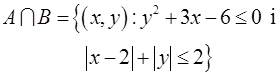
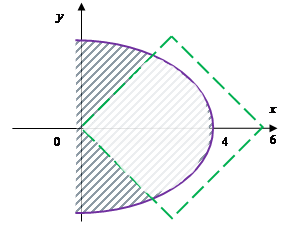 Різниця множин
Різниця множин 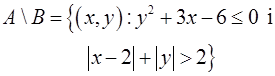


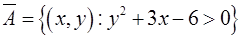
 Доповнення до множини
Доповнення до множини 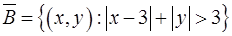
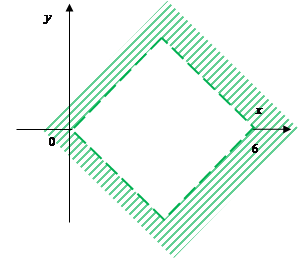
 Симетрична різниця множин
Симетрична різниця множин 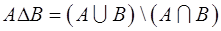
 за властивістю
за властивістю  ;
; за законом де Моргана
за законом де Моргана  ;
; за властивостями
за властивостями  ,
,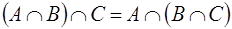 ;
; за властивістю
за властивістю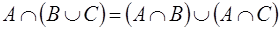 ;
; за властивостями
за властивостями 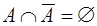 ,
, ,
,  ;
;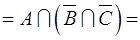 за властивістю
за властивістю за властивістю
за властивістю  .
.

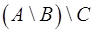

 , якщо
, якщо ;
;  ;
;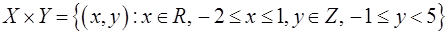 .
.
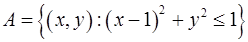

 3. Домашне завдання:
3. Домашне завдання: