Критерии. Отсутствие объяснения, почему в двух разных наборах различаются и книги, и обложки, не штрафуется.
Отсутствие объяснения, почему в двух разных наборах различаются и книги, и обложки, не штрафуется. Рассмотрение частного случая оценивается в 0 баллов.
Пример решения, оцениваемого в 7 баллов: «Может. Посчитаем количество комбинаций книжка+обложка. 20 книжек и к каждой можно приложить одну из 20 обложек. Таких вариантов 20·20=400. А теперь посчитаем, сколько могут стоить эти комплекты. От 7 евро +10 центов до 10 евро+1 евро. Значит, различных цен комплектов 1100-710+1=391. Получается, что на какие-то комплекты цены будут совпадать.»
(9-10) 6C. Решите систему уравнений:
Решение: Введем обозначения: Эта вспомогательная система имеет два решения: (1) Вернувшись к исходным переменным, имеем: (1) Решая полученные системы (можно снова воспользоваться теоремой Виета), получаем для каждой из них по 2 решения: (1) Итак, исходная система имеет ровно 4 решения: (1;5), (5;1), (2;3), (3;2).
Критерии: 1) Верный ответ без каких-либо объяснений — 1 балл. 2) Одна арифметическая ошибка в одной из двух последних систем (в результате получились 4 решения, из которых два верны, два неверны) — 5 баллов. 3) Арифметические ошибки, приводящие к другим последствиям — максимум 2 балла. 4) Из каждых двух решений указано только одно (а симметричное забыто) — 2 балла. 5) Объяснять, почему каждая из вспомогательных систем имеет только два решения (и откуда они берутся), не обязательно.
(11) 6D. Пусть p1,..., pn — различные простые числа. Пусть S — сумма всевозможных произведений четного (ненулевого) количества различных простых из этого набора. Докажите, что S+1 делится на 2n-2.
Решение. Рассмотрим произведения A=(1−p1)(1−p2)...(1−pn) и B=(1+p1)(1+p2)...(1+pn). Заметим, что при раскрытии скобок все произведения с чётным (в том числе нулевым) количеством множителей войдут в них с плюсом, а произведения нечётного числа множителей — с разными знаками. Поэтому если эти два произведения сложить, то останутся только произведения чётного числа множителей, причём каждое появится дважды. Итак, A+B = 2(S+1) (единица — это произведение нуля множителей, которое входит в A и B, но по определению не входит в S). Заметим, что все числа p1,..., pn различны, поэтому все они, кроме, быть может, одного (двойки) — нечётны. Поэтому в произведении A=(1−p1)(1−p2)...(1−pn) все множители, кроме, быть может, одного — чётные, и оно делится на 2n−1. Аналогично и B делится на 2n−1, поэтому S+1=(A+B)/2 делится на 2n−2.
Критерии. Забыли про существование чётного простого числа (двойки) — 5 баллов.
|
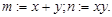Тогда система примет вид: 
.
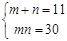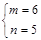и (2) 
и (2)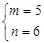 
.
и 
; (2) 
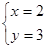и 
.
