Критерии.
Продвижения: Встречаются соображения о том, что у некоторых (или у всех) кубиков должны быть покрыты лаком грани 1, 2, 3 и 4, а иначе ничего не получится — не менее 1 балла. Верно составлено неравенство — 2 балла. В дополнение к этому 1 балл даётся за ответ 21 с примером. (Только за ответ 21 ничего не даётся).
Нечёткости: За решение в стиле «В худшем случае на каждом торцевом кубике покрыты лаком 10 очков, а на каждом из остальных 15, тогда для 20 кубиков всё плохо (приведён пример), а для 21 кубика всё в порядке (приведён пример)» — 5 баллов. За решение в стиле «В худшем случае на каждом торцевом кубике покрыты лаком 10 очков, а на каждом из остальных 15, а среднее 10,5, тогда каждый торцевой кубик должен компенсироваться девятью внутренними, тогда будет ровно половина; а надо, чтобы непокрытых лаком было больше, поэтому добавим ещё один внутренний» можно ставить полный балл. Если всё правильно, но в ответе указано 20, а не 21 (и, возможно, участник решает нестрогое неравенство), то один балл снимается. В полном решении (типа приведённых выше) можно не упоминать, что пример на 21 существует, поскольку и так ясно, как он строится.
Задача 5 (5-6) A. В одном доме провели перепись населения. Выяснилось, что в каждой квартире живет супружеская пара (мать и отец) и в каждой семье есть хотя бы один ребенок. У каждого мальчика в доме есть сестра, но всего мальчиков больше, чем девочек. Детей же в доме меньше, чем взрослых. Докажите, что в результаты переписи вкралась ошибка.
Решение. Во-первых, заметим, что в каждой семье есть хотя бы одна девочка (поскольку у любого мальчика есть сестра). Тогда девочек хотя бы столько же, сколько супружеских пар, а мальчиков больше, чем супружеских пар. Складывая все вместе, получаем, что детей больше, чем взрослых.
Критерии. По общим правилам. Замены типа «больше» на «не меньше» — 5 баллов.
(7[8,9]) B. По кругу в каком-то порядке выписаны числа от 1 до 77 [до 88, до 99]. Какова минимально возможная сумма модулей разностей между соседними числами?
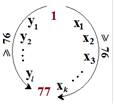
Решение (для 77 чисел). Заметим, что где-то в круге стоят числа 1 и 77. Рассмотрим «путь» от 1 до 77 по часовой стрелке: 1, x1, x2, …, xk, 77. Заметим, что при прождении по этому пути число изменяется на 76, поэтому сумма модулей разностей не меньше 76 (формально: |77-xk| + |xk-xk-1| + … + |x2-x1| + |x1-1| >= |77-1| = 76). Теперь рассмотрим путь между числами 1 и 77 «с другой стороны» (против часовой стрелки); сумма модулей разностей, стоящих там, также не меньше 76. Поэтому общая сумма модулей разностей не меньше 152. Результат 152 достигается (например, при расстановке чисел по порядку).
Критерии. Только ответ — 1 балл. Ответ с примером — 2 балла. Оценка с верным ответом, но без упоминания примера — снимаем 2 балла (?) Арифметическая ошибка (или ответ, допустим, 77·2 вместо 76·2) — минус балл. К формулировкам доказательства не придираемся (достаточно картинки с двумя стрелочками в разные стороны). Почему сумма разностей при переходе от 1 к 77 не меньше 76, объяснять не обязательно.
(10-11) C. СН — высота в треугольнике АВС, а О — центр его описанной окружности. Из точки С опустили перпендикуляр на АО, а его основание обозначили через Т. Наконец, через М обозначили точку пересечения НТ и ВС. Найдите отношение длин отрезков ВМ и СМ.
|

 Ответ. 152 (для 7 класса), 174 (для 8 класса), 196 (для 9 класса)
Ответ. 152 (для 7 класса), 174 (для 8 класса), 196 (для 9 класса)