Показательные уравнения
1. Балдин, К.В. Управленческие решения: теория и технология принятия: Учебник для вузов / К. В. Балдин, С. Н. Воробьев. - М.: Проект, 2011. - 300с.; 2. Воробьев С.Н., Уткин В.Б., Балдин К.В. Управленческие решения: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2012. – 317 с.; 3. Ивасенко, А.Г. Разработка управленческих решений: учебное пособие / А.Г.Ивасенко, Я.Н.Никонова, Е.Н.Плотникова. – М.: КНОРУС, 2010. – 168 с.; 4. Коротков Э.М. Исследование систем управления: Учебник. – М.:ДЕКА, 2013. – 416 с.; 5. Котенко А.Н. Влияние системы «таргет-костинг» на результаты деятельности коммерческой организации //Экономика и производство. 2010. - №3. – С. 47 – 50; 6. Кузнецова, Н. В. Управленческие решения: учеб.-метод. комплекс / Н. В. Кузнецова; МаГУ. - Магнитогорск: Изд-во МаГУ, 2012. - 180 с.; 7. Литвак, Б.Г.Разработка управленческого решения: Учебник для вузов / Б. Г. Литвак. - М.: Дело, 2010. - 392с.; 8. Лифшиц, А.С. Управленческие решения: учебное пособие / А.С.Лифшиц. – М.: КНОРУС, 2011. – 248 с.; 9. Лукичева Л. И. Управленческие решения: учебник для вузов / Л. И. Лукичева, Д. Н. Егорычев; под ред. Ю. П. Анискина. - М.: Омега-Л, 2010. - 383 с.; 10. Орлов, А. И. Принятие решений. Теория и методы разработки управленческих решений: учеб. пособие для вузов / А. И. Орлов. - М. [и др.]: МарТ, 2011. - 495 с.; 11. Ременников В.В. Разработка управленческого решения: Учеб.пособие для вузов. – М.Юнити-ДАНА, 2011. – 140 с.; 12. Рогожин С.В., Рогожина Т.В. Исследования систем управления: учебник – М.: Изд-во «Экзамен», 2013. – 320 с.; 13. Самойлова А.Н. Оценка эффективности управления человеческими ресурсами организации //Экономический анализ: теория и практика. 2010. - №11 (92) – С. 38 – 44; 14. Смирнов, Э.А. Управленческие решения: Учебник для вузов. / Э.А.Смирнов. – М.: РИОР, 2010. – 362 с.; 15. Юкаева, В. С. Управленческие решения: учеб. пособие [для вузов] / В. С. Юкаева. - 3-е изд. - М.: Дашков и К, 2010. - 322 с. Решение показательных и логарифмических уравнений Показательные уравнения Простейшие показательные уравнения имеют вид: Уравнение Если в уравнении присутствуют показательные функции с разными основаниями, можно попытаться привести их к одному и тому же основанию. То же относится и к логарифмическим уравнениям. 1. 2.
|

 .
. при
при  и при
и при  корней не имеет, так как показательная функция всегда положительна.
корней не имеет, так как показательная функция всегда положительна.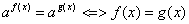 при
при 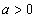 ,
,  ;
; .
.


