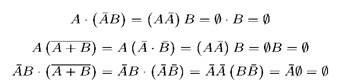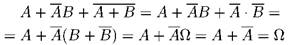Решение. Видим, что в нашем случае линейная корреляционная связь очень сильная.

Видим, что в нашем случае линейная корреляционная связь очень сильная.

 

Так как Выборочный коэффициент корреляции r положителен, то увеличение одной величины приводит к увеличению другой.

 

Для проверки статистической значимости корреляционной зависимости величин воспользуемся критерием Стьюдента:

.

Для уровня значимости a = 0,1 и числа степеней свободы равным n –2 = 3 по таблице в учебнике, найдем критическое значение критерия Стьюдента
t_{a ; (n –2)} = t_{0,1; 3} = 2,35.

 

Так как, t_расчет > t_{a(n –2)}, то принимаем гипотезу Н. Вывод: корреляционная связь между признаками статистически значимая.

Решение.

1. Ω = {11,12,13,14,15,16, 21, 22,..., 66},

2. Ω = {2,3,4,5,6, 7,8,9,10,11,12}

3. ● A = {16,61,34, 43, 25, 52};

● B = {11,12, 21,13,31,14, 41,15, 51,16, 61}

● C = {12, 21,36,63,45, 54,33,15, 51, 24,42,66}.

● D = {СУММА ОЧКОВ РАВНА 2 ИЛИ 3 };

● E = {СУММА ОЧКОВ РАВНА 10}.

Задача 3Даны две электрические схемы:

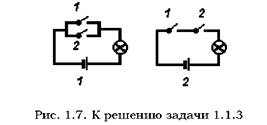
Описать событие: С = {ЦЕПЬ ЗAМКНУТA} для каждого случая.

Решение. Введем обозначения: событие A - контакт 1 за­мкнут; событие В - контакт 2 замкнут; событие С - цепь замкнута, лампочка горит.

1. Для параллельного соединения цепь замкнута, когда хотя бы один из контактов замкнут, поэтому С = A + В;

2. Для последовательного соединения цепь замкнута, ко­гда замкнуты оба контакта, поэтому С = A · В.

Задача. 1.1.4 Составлены две электрические схемы:

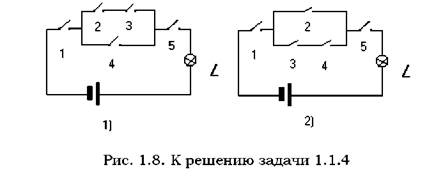
Событие A — цепь замкнута, событие A _i - i –й кон­такт замкнут. Для какой из них справедливо соотноше­ние

A₁ · (A₂ + A₃ · A₄) · A₅ = A?

Решение. Для первой схемы A = A₁ · (A₂ · A₃ + A₄ · A₅), так как параллельному соединению соответствует сумма собы­тий, а последовательному соединению — произведение событий. Для второй схемы A = A1 • (A₂ + A₃ • A₄ • A₅). Сле­довательно, данное соотношение справедливо для второй схемы.

 

Задача. 1.1.5 Упростить выражение (A + B)(B + C)(C+ A).

Решение. Воспользуемся свойствами операций сложения и умножения событий.

(A + B)(B + C)(A + C) =

(AB + AC + B B + BC)(A + C) =

= (AB + AC + B + BC)(A + C) =

(AB + AC + B)(A + C) = (B + AC)(A + C) =

= BA + BC + ACA + ACC = B A + BC + AC.

Задача. 1.1.6 Доказать, что события A,AB и A+B обра­зуют полную группу.

 

Решение. При решении задачи воспользуемся свойства­ми операций над событиями. В начале покажем, что эти события попарно несовместны.

A теперь покажем, что сумма этих событий дает простран­ство элементарных событий.

 

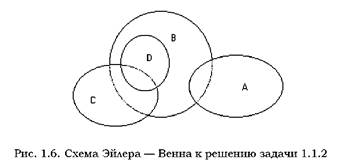
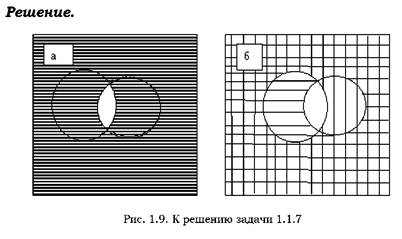
Задача. 1.1.7 С помощью схемы Эйлера–Венна проверить правило де-Моргана:

 

___ _ _

AB = A+B.

__

а) Заштриховано событие AB.

__ __

б) Событие A — вертикальная штриховка; событие B — горизонтальная штриховка. Событие

__ __

{A+B} — заштрихованная область.

Из сопоставления рисунков а) и в) следует:

___ _ _

AB = A+B.

 

Задача. 1.2.1 Сколькими способами можно рассадить 8 человек:

1. В один ряд?

2. За круглым столом?
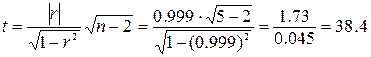