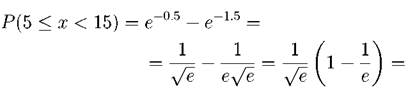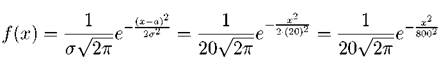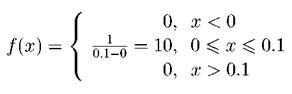Решение. По формуле (2.12) находим математическое ожидание:
По формуле (2.12) находим математическое ожидание: M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 10 · 0.2 + 20 · 0.15 + 30 · 0.25 + 40 · 0.4 = 28.5 M[2X + 5] = 2M[X] + M[5] = 2M[X] + 5 = 2 · 28.5 + 5 = 62. По формуле (2.19) найдем дисперсию:
Задача. 2.2.2 Найти математическое ожидание, дисперсию и среднее квадратичное отклонение непрерывной случайной величины X, функция распределения которой . Решение. Найдем плотность вероятности:
Математическое ожидание найдем по формуле (2.13):
Дисперсию найдем по формуле (2.19): Найдем сначала математическое ожидание квадрата случайной величины:
Тогда Среднее квадратичное отклонение
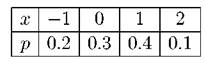
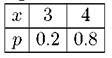
Задача. 2.2.3 Дискретная случайная величина X имеет ряд распределения:
Найти математическое ожидание и дисперсию случайной величины Y = eX. Решение. M[Y] = M[ eX ] = e-- 1 · 0.2 + e0 · 0.3 + e1 · 0.4 + e2 · 0.1 = = 0.2 · 0.3679 + 1 · 0.3 + 2.71828 · 0.4 + 7.389 · 0.1 = 2.2. D[Y] = D[ex] = M[(eX)2 — M2 [ e X] = [(e-1)2 • 0.2 + (e0)2 • 0.3 + (e1)2 • 0.4 + (e2)2 • 0.1] — (2.2)2 = = (e--2 • 0.2 + 0.3 + e2 • 0.4 + e4 • 0.1) — 4.84 = 8.741 — 4.84 = 3.9. Задача. 2.2.4 Дискретная случайная величина X может принимать только два значения x1 и x2, причем x1 < x2. Известны вероятность p1 = 0.2 возможного значения x1, математическое ожидание M[X] = 3.8 и дисперсия D[X] = 0.16. Найти закон распределения случайной величины. Решение. Так как случайная величина X принимает только два значения x1 и x2, то вероятность p2 = P(X = x2) = 1 - p1 = 1 - 0.2 = 0.8. По условию задачи имеем: M[X] = x1p1 + x2p2 = 0.2x1 + 0.8x2 = 3.8; D[X] = (x21p1 + x22p2) - M2[X] = (0.2x21 + 0.8x22) - (0.38)2 = 0.16. Таким образом получили систему уравнений:
Условию x1<x2 удовлетворяет решение x1 = 3. x = 4. Поэтому искомый закон распределения имеет вид: Задача. 2.2.5 Случайная величина X подчинена закону распределения, график плотности которого имеет вид:
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение. Решение. Найдем дифференциальную функцию распределения f(x). Вне интервала (0, 3) f(x) = 0. На интервале (0, 3) график плотности есть прямая с угловым коэффициентом k = 2/9, проходящая через начало координат. Таким образом, Математическое ожидание:
Найдем дисперсию и среднее квадратичное отклонение:
Задача. 2.2.6 Найти математическое ожидание и дисперсию суммы очков, выпадающих на четырех игральных кубиках при одном бросании. Решение. Обозначим A — число очков на одном кубике при одном бросании, B – число очков на втором кубике, C — на третьем кубике, D — на четвертом кубике. Для случайных величин A, B, C, D закон распределения Тогда M[A] = M[B] = M[C] = M[D] = (1+2+3+4+5+6) / 6 = 3.5
Задача. 2.3.1 Вероятность того, что частица, вылетевшая из радиоактивного источника, будет зарегистрирована счетчиком, равна 0.0001. За время наблюдения из источника вылетело 30000 частиц. Найти вероятность того, что счетчик зарегистрировал: 1. ровно 3 частицы; 2. ни одной частицы; 3. не менее 10 частиц. Решение. По условию п = 30000, p = 0.0001. События, состоящие в том, что частицы, вылетевшие из радиоактивного источника, зарегистрированы, независимы; число п велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона:
Задача. 2.3.2 В партии 5% нестандартных деталей. Наудачу отобраны 5 деталей. Написать закон распределения дискретной случайной величины X — числа нестандартных деталей среди пяти отобранных; найти математическое ожидание и дисперсию. Решение. Дискретная случайная величина X — число нестандартных деталей — имеет биномиальное распределение и может принимать следующие значения: x1 = 0, x2 = 1, x3 = 2, x4 = 3, x5 = 4, x6 = 5. Вероятность нестандартной детали в партии p = 5/100 = 0.05. Найдем вероятности этих возможных значений:
Напишем искомый закон распределения:
Найдем числовые характеристики:
+ 3 • 0.0011281 + 4 • 0.0000297 + 5 • 0.0000003 = 0.2499999 ≈ 0.250 или M[X] = n • p = 5 • 0.05 = 0.25. D[X] = M[X2 ] – M2 [X] = 02 • 0.7737809 + 12 • 0.2036267+ + 22 • 0.0214343 + 32 • 0.0011281 + 42 • 0.0000297 + 52 • 0.0000003- 0.0625 = = 0.2999995 - 0.0625 = 0.2374995 ≈ 0.2375 или D[X] = n • p • (1 - p) = 5 • 0.05 • 0.95 = 0.2375. Задача. 2.3.3 Время обнаружения цели радиолокатором распределено по показательному закону
где 1/ λ = 10 сек. - среднее время обнаружения цели. Найти вероятность того, что цель будет обнаружена за время от 5 до 15 сек. после начала поиска. Решение. Вероятность попадания случайной величины X в интервал (5, 15) найдем по формуле (2.8):
При
= 0.6065(1 - 0.3679) = 0.6065 • 0.6321 = 0.3834 Задача. 2.3.4 Случайные ошибки измерения подчинены нормальному закону с параметрами a = 0, σ = 20 мм. Записать дифференциальную функцию распределения f(x) и найти вероятность того, что при измерении допущена ошибка в интервале от 5 до 10 мм. Решение. Подставим значения параметров a и σ в дифференциальную функцию распределения (2.35):
По формуле (2.42) найдем вероятность попадания случайной величины X в интервале [0, 5):
Здесь значения функции Лапласа взяты по таблице. Задача. 2.3.5 Цена деления шкалы амперметра равна 0.1 ампера. Показания амперметра округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0.03 ампера. Найти математическое ожидание, дисперсию ошибки округления отсчета и функцию F(x). Решение. Ошибку округления отсчета можно считать распределенной равномерно на [0; 0.1], т.е. a = 0, b = 0.1. Тогда дифференциальная функция распределения f(x) будет иметь вид
|

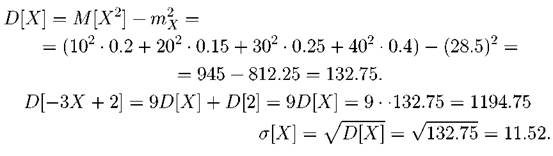

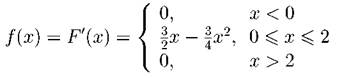
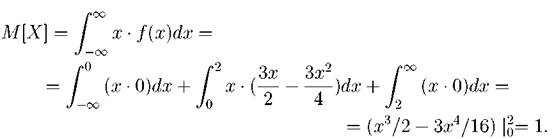
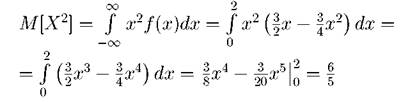
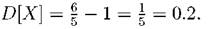
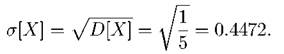
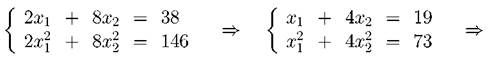
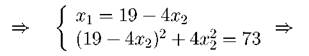


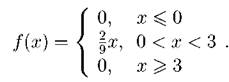
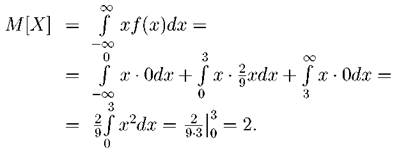

 один.
один.
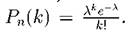 Найдем λ: λ = п p = 30000 • 0.0001 = 3 = М[Х]. Искомые вероятности:
Найдем λ: λ = п p = 30000 • 0.0001 = 3 = М[Х]. Искомые вероятности: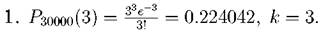



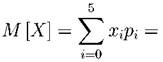 0 • 0.7737809 + 1 • 0.2036267 + 2 • 0.0214343+
0 • 0.7737809 + 1 • 0.2036267 + 2 • 0.0214343+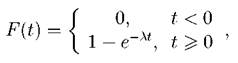
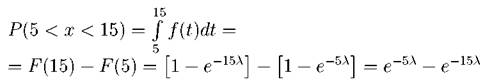
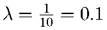 получаем
получаем