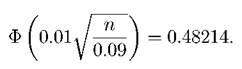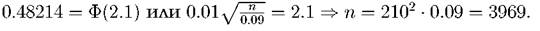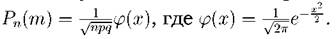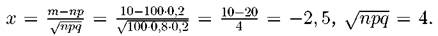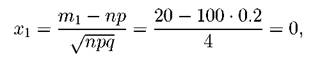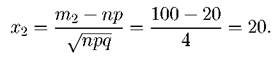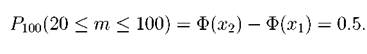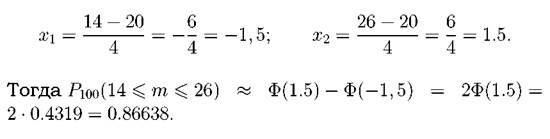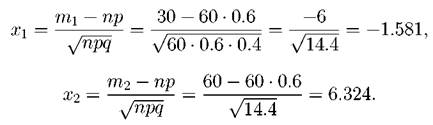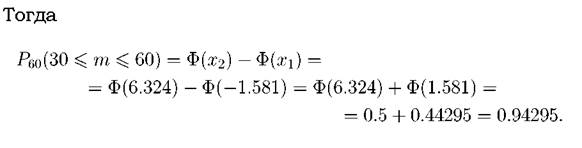Решение. Требуемое число n найдем по формуле (1.25)
Требуемое число n найдем по формуле (1.25). Имеем: p = 1.1; q = 0.9; P = 0.96428. Подставим данные в формулу:
Откуда находим
По таблице значений функции Φ(x) находим, что
Задача. 1.5.5 Вероятность выхода из строя за время Т одного конденсатора равна 0.2. Определить вероятность того, что за время Т из 100 конденсаторов выйдут из строя 1. ровно 10 конденсаторов; 2. не менее 20 конденсаторов; 3. менее 28 конденсаторов; 4. от 14 до 26 конденсаторов. Решение. Имеем п = 100, p = 0.2, q = 1 - p = 0.8. 1. Ровно 10 конденсаторов. Так как п велико, воспользуемся локальной теоремой Муавра - Лапласа: Вычислим Так как функция φ(х) — четная, то φ(-2,5) = φ(2,50) = 0,0175 (находим по таблице значений функции φ(х). Искомая вероятность
2. Не менее 20 конденсаторов; Требование, чтобы из 100 конденсаторов из строя вышли не менее 20, означает, что из строя выйдут либо 20, либо 21,..., либо 100. Таким образом, т1 = 20, т 2 =100. Тогда
По таблице значений функции Φ(x) найдем Φ(x1) = Φ(0) = 0, Φ(x2) = Φ(20) = 0.5. Искомая вероятность:
3. Менее 28 конденсаторов;
(здесь было учтено, что функция Лапласа Ф(x) - нечетная). 4. От 14 до 26 конденсаторов. По условию m1= 14, m2 = 26.
Задача. 1.5.6 Вероятность появления некоторого события в одном опыте равна 0.6. Какова вероятность, что это событие появиться в большинстве из 60 опытов? Решение. Количество m появлений события в серии испытаний находится в промежутке [0; 60]. «В большинстве опытов» означает, что m принадлежит промежутку[30, 60.] По условию n = 60, p = 0.6, q = 0.4, m1 = 30, m2 = 60. Вычислим x1 и x2:
|