1. Савельев И.В. Курс общей физики: Учебник: В 3 т.– М.: Наука, 1988.
2. Трофимова Т.И. Курс физики: Учебное пособие для вузов. – М.: Наука, 2000.
3. Зисман О.И., Тодес Т.Н. Курс физики: Учебник: В 3 т.– М.: Высшая школа, 1974.
Учебное издание
Составители: ГРЕЙСУХ ГРИГОРИЙ ИСАЕВИЧ
СТЕПАНОВ СЕРГЕЙ АЛЕКСЕЕВИЧ
НЕДОРЕЗОВ ВАЛЕРИЙ ГРИГОРЬЕВИЧ
ИЗУЧЕНИЕ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ
НА МАШИНЕ АТВУДА
И ЕЕ КОМПЬЮТЕРНОЙ МОДЕЛИ
Методические указания
к лабораторной работе № 3
Редактор М.А.Сухова
Верстка А.В.Филиппова
___________________________________
Лицензия ЛР № 020454 от 25.04.97.
Подписано в печать.22.04.02.Формат 60х84/16.
Бумага офсетная. Печать офсетная.
Усл.печ.л.0,87. Уч.-изд.л.0,94.Тираж 80 экз.
Заказ №62
______________________________________________
Издательство ПГАСА.
Отпечатано в цехе оперативной полиграфии ПГАСА.
440028, г.Пенза,ул.Г.Титова,28
ЛАБОРАТОРНАЯ УСТАНОВКА
 Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Основой машины Атвуда (рис. 1) является вертикальная штанга 1 со шкалой. На верхнем торце штаги закреплен легкий блок 2, способный вращаться с незначительным трением. Через блок перекинута тонкая нить с прикрепленными грузами 3 одинаковых масс 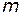 . С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
. С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
 Если на правый груз положить перегрузок массой
Если на правый груз положить перегрузок массой  , то система грузов, связанных нитью, начнет двигаться с некоторым ускорением
, то система грузов, связанных нитью, начнет двигаться с некоторым ускорением  (рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
(рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
Направив ось  вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
для правого груза
 , (1)
, (1)
для левого груза
 , (2)
, (2)
где  – ускорение свободного падения;
– ускорение свободного падения;
 – сила натяжения нити.
– сила натяжения нити.
Совместное решение уравнений (1) и (2) дает
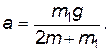 (3)
(3)
Из формулы (3) следует, что ускорение системы прямо пропорционально результирующей внешних сил, действующих на систему (в данном случае – силе тяжести перегрузка массой 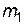 ), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):

Рис. 3
Из рисунка видно, что результирующая внешних сил, приложенных к системе «грузы – нить», равна в соответствии со вторым законом Ньютона
 . (4)
. (4)
Формулы (3) и (4) справедливы лишь при условии принятых выше допущений. Здесь отметим, что масса блока и дополнительные внешние силы (сила трения в блоке и сила сопротивления воздуха) уменьшают величину ускорения.
Формулы кинематики для пути и скорости при прямолинейном равноускоренном движении имеют вид
 , (5)
, (5)
где 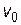 – начальная скорость тела;
– начальная скорость тела;
 – время ускоренного движения.
– время ускоренного движения.
Используя формулы (5) и полагая в них  , ускорение тела можно найти по любой из двух формул:
, ускорение тела можно найти по любой из двух формул:
 , (6)
, (6)
 . (7)
. (7)
Сопоставление значений ускорения, вычисленных по формулам (6) и (7), с величиной ускорения, рассчитанного по формуле (3), позволяет проверить кинематические формулы пути и скорости тела при равноускоренном движении, что и составляет содержание первых двух заданий работы.

 Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».
Наиболее очевидный путь исследования прямолинейного движения тел под действием силы тяжести – это изучение свободного падения. Однако этому методу существенно препятствует большая величина ускорения при свободном падении. Действительно, при малой высоте прибора время падения тела составит малые доли секунды, и ошибки фиксации начала и конца движения окажутся соизмеримыми с временем падения. При большой же высоте прибора падающее тело наберет значительную скорость, и сила сопротивления воздуха окажется соизмеримой с силой тяжести, которая при малых скоростях движения возрастает пропорционально скорости тела. Это, в свою очередь, приведет к уменьшению ускорения. Преодолеть указанные трудности (уменьшив ускорение до приемлемых величин) позволяет устройство, получившее название «машина Атвуда».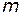 . С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение.
. С помощью тормоза 4 грузы могут удерживаться в состоянии покоя. На штанге крепятся два кронштейна 5 и 6 с фотоэлектрическими датчиками. Фотоэлектрический датчик верхнего кронштейна формирует импульс напряжения, сигнализирующий о начале движения, датчик нижнего кронштейна – импульс, сигнализирующий о конце движения. Верхний кронштейн – подвижный, его можно перемещать вдоль штанги и фиксировать в любом положении, задавая таким образом длину пути груза. Нижний кронштейн – неподвижный, он оснащен платформой с резиновым амортизатором, в которую ударяется правый груз, завершая движение. Если на правый груз положить перегрузок массой
Если на правый груз положить перегрузок массой  , то система грузов, связанных нитью, начнет двигаться с некоторым ускорением
, то система грузов, связанных нитью, начнет двигаться с некоторым ускорением  (рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы.
(рис. 2). Пренебрегая силой сопротивления воздуха, массой блока и силой трения в блоке, а также полагая нить нерастяжимой и невесомой, можно считать, что на каждый груз действуют две силы: сила тяжести груза и сила натяжения нити. Причем силы натяжения, действующие на оба груза, в этом случае одинаковы. вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения:
вертикально вниз и воспользовавшись вторым законом Ньютона, можно записать для каждого из грузов следующие уравнения движения: , (1)
, (1) , (2)
, (2) – ускорение свободного падения;
– ускорение свободного падения; – сила натяжения нити.
– сила натяжения нити.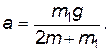 (3)
(3)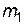 ), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
), и обратно пропорционально массе всей системы. В этом легко убедиться, записав второй закон Ньютона для всей системы «грузы – нить» в целом. При этом для наглядности систему целесообразно развернуть вдоль одной горизонтальной оси, выбрав ее направление, например, от одиночного груза к грузу с перегрузком (рис. 3):
 . (4)
. (4) , (5)
, (5)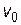 – начальная скорость тела;
– начальная скорость тела; – время ускоренного движения.
– время ускоренного движения. , ускорение тела можно найти по любой из двух формул:
, ускорение тела можно найти по любой из двух формул: , (6)
, (6) . (7)
. (7)


