Расчет загрузки элементов горловины всеми передвижениями
| №п/п
| Наименование передвижений
| 
| Загрузка элемента
| | I
| II
| III
| IV
| 
| 
| 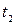
| 
| 
| 
| 
| 
| | 1.
| Прием четного пассажирского поезда:
|
|
|
|
|
|
|
|
|
| | на 3-й путь
|
| 9,2
| 18,4
| 9,2
| 18,4
| –
| –
| –
| –
| | на 5-й путь
|
| 10,3
| 30,9
| 10,3
| 30,9
| –
| –
| 10,3
| 30,9
| | 2.
| Отправление нечетного пассажирского поезда:
|
|
|
|
|
|
|
|
|
| | с 3-го пути
|
| –
| –
| 6,6
| 13,2
| –
| –
| –
| –
| | с 5-го пути
|
| –
| –
| 7,7
| 23,1
| –
| –
| 7,7
| 23,1
| | 3.
| Прием четного пригородного поезда:
|
|
|
|
|
|
|
|
|
| | на 3-й путь
|
| 8,6
| 8,6
| 8,6
| 8,6
| –
| –
| –
| –
| | на 5-й путь
|
| 9,7
| 19,4
| 9,7
| 19,4
| –
| –
| 9,7
| 19,4
| | 4.
| Отправление нечетного пригородного поезда:
|
|
|
|
|
|
|
|
|
| | с 3-го пути
|
| –
| –
| 6,3
| 6,3
| –
| –
| –
| –
| | с 5-го пути
|
| –
| –
| 7,4
| 14,8
| –
| –
| 7,4
| 14,8
| | 5.
| Прием четного грузового поезда:
|
|
|
|
|
|
|
|
|
| | на II-й путь
|
| 8,2
| 16,4
| –
| –
| –
| –
| –
| –
| | на 4-й путь
|
| 9,4
| 18,8
| –
| –
| 9,4
| 18,8
| –
| –
| | на 6-й путь
|
| 10,4
| 20,8
| –
| –
| 10,4
| 20,8
| –
| –
| | 6.
| Отправление нечетного грузового поезда:
|
|
|
|
|
|
|
|
|
| | с I-го пути
|
| –
| –
| 6,5
| 13,0
| –
| –
| –
| –
| | с 4-го пути
|
| 8,6
| 17,2
| 8,6
| 17,2
| 8,6
| 17,2
| –
| –
| | с 6-го пути
|
| 9,6
| 19,2
| 9,6
| 19,2
| 9,6
| 19,2
| –
| –
|
Продолжение таблицы П.4.5
| №п/п
| Наименование передвижений
| 
| Загрузка элемента
| | I
| II
| III
| IV
| 
| 
| 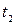
| 
| 
| 
| 
| 
| | 7.
| Маневры по четному главному пути
|
| 5,9
| 11,8
| –
| –
| –
| –
| –
| –
| | 8.
| Маневры по нечетному главному пути
|
| –
| –
| 6,1
| 12,2
| –
| –
| –
| –
| 
| 181,5
| 196,3
|
| 88,2
|
Так как  существующие устройства не смогут обеспечить заданный объем движения поездов. существующие устройства не смогут обеспечить заданный объем движения поездов.
П.4.2 Расчет загрузки горловины станции при централизованных стрелках
П.4.2.1 Разбивка на расчетные элементы горловины станции
Разбивка на расчетные элементы при электрической централизации приведена на рис. П.4.2. Число элементов определено с учетом применения посекционного размыкания маршрутов.
П.4.2.2 Определение длины расчетных элементов
Длина расчетных элементов при электрической централизации рассчитывается также по ординатам стрелок и сигналов. Для примерной станции длина элементов приведена в табл. П.4.6.

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
Схема рефлекторной дуги условного слюноотделительного рефлекса При неоднократном сочетании действия предупреждающего сигнала и безусловного пищевого раздражителя формируются...
Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны Уравнением упругой волны называют функцию , которая определяет смещение любой частицы среды с координатами относительно своего положения равновесия в произвольный момент времени t...
|
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК...
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
|
|




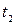






 существующие устройства не смогут обеспечить заданный объем движения поездов.
существующие устройства не смогут обеспечить заданный объем движения поездов.


