Решение. Для оперативного принятия управленческих решений необходимо, чтобы информация была структурирована и отображала набор показателей по различным уровням
Хранение всей истории создания отчетов различных разрезах на каждом уровне, вплоть до директивных ключевых показателей, и оценивать бизнес с различных сторон: в разрезе потребителей, линеек продуктов, регионов и других категорий. Модуль позволяет проводить анализ сравнительных отчетных данных различных предприятий и направлений деятельности.
Решение Имеем:
поэтому согласно (1.37) получаем ответ. Ответ.
Тема 4.12. Производные неявной функции Если у есть неявная функция от х, т.е. задана уравнением F(x,y)=0, не разрешенным относительно у, то для нахождения производной нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно у'. Пример. Найти производную неявной функции х2+у2-4х-10у+4=0. Дифференцируя по х, получаем 2х+2у *у' -4-10у'=0. Выражаем у', имеем:
Задачи для самопроверки.
Пример. Продифференцировать выражения Решение. Так как y – это функция от x, то При дифференцировании второго выражения выносим константу за знак производной и действуем как в предыдущем случае (здесь f – функция синуса, g(x) = y):
Для третьего выражения применяем формулу производной произведения:
Последовательно применяя правила, продифференцируем последнее выражение:
Найти производную неявной функции
|

 Для оперативного принятия управленческих решений необходимо, чтобы информация была структурирована и отображала набор показателей по различным уровням представления. Возможность использования неограниченного набора атрибутов и аналитики позволяет выполнять анализ в
Для оперативного принятия управленческих решений необходимо, чтобы информация была структурирована и отображала набор показателей по различным уровням представления. Возможность использования неограниченного набора атрибутов и аналитики позволяет выполнять анализ в
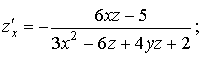


 по x, считая y функцией от x.
по x, считая y функцией от x. - это сложная функция. Ее можно условно представить как f(g(x)), где f – функция возведения в куб, а g(x) = y. Тогда, по формуле производной сложной функции имеем:
- это сложная функция. Ее можно условно представить как f(g(x)), где f – функция возведения в куб, а g(x) = y. Тогда, по формуле производной сложной функции имеем:  .
.


 .
.


