МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Рассмотрим решение задачи №2 на примере.
Рассмотрим решение задачи №2 на примере. 1. Пусть в таблице 6.3 задано
Рассчитаем угловую частоту ω;для первой гармоники (см. 5.6)
ω = 2π f(1) = 2 π; • 80 = 502 1/c.
Угловая частота третьей гармоники напряжения
3 ω = 1506 1/с.
В соответствии с таблицей 6.3 и проведёнными расчётами приложенное к электрической цепи напряжение имеет вид
u(t) = 50 + 320 sin(502t + 270) + 100 sin(1506t + 440).
То есть приложенное к электрической цепи напряжение содержит · постоянную составляющую (частота равна нулю f = = 0; ω;= 0)
U0 = 50 В;
· первую гармонику с частотой f(1) = 80 Гц (ω = 502 1/c)
u1 (t) = 320 sin(502t + 270) В;
· третью гармонику с частотой в три раза большей f(3) = 240 Гц (3 ω = 1506 1/с)
u3 (t) = 100 sin(1506t + 440).
2. В таблице 6.4 задан вид элементов, входящих в схему пассивных двухполюсников электрической цепи. Пусть дано.
Данным таблицы соответствует схема замещения рис. 6.6.
Рис. 6.6. Схема замещения электрической цепи
3. Определение сопротивлений элементов электрической цепи для каждой из гармоник. Пусть по таблице 6.5 имеем следующие данные.
Параметры элементов электрической цепи
· ·
Определение сопротивлений элементов электрической цепи для каждой из гармоник проводится в соответствии со следующими положениями. · Сопротивления всех резисторов не зависит от частоты и остаётся постоянным для каждой из гармоник. R1 = 11 Ом; R2 = 15 Ом; R3 = 4 8 Ом.
· Поскольку частота постоянного тока равна нулю f = = 0, то и сопротивление катушки индуктивности постоянному току также равно нулю.
XL1(0) = ωL1 = 2πf= L1 = 2π;• 0 • 127,4 • 10-3 = 0
· А вот сопротивление конденсатора постоянному току равно бесконечности.
XC2(0) =
· Для первой гармоники Сопротивление катушки индуктивности
XL1(1) = ωL1 = 502 • 127,4 • 10-3 = 64 Ом.
Сопротивление конденсатора
XC2(1) =
· Для третьей гармоники Сопротивление катушки индуктивности
XL1(3) = 3ωL1 = 3 XL1(1) = 192 Ом.
Сопротивление конденсатора
XC2(3) =
Все проведённые расчёты сведём таблицу 6.6.
Таблица 6.6. Сопротивления элементов электрической цепи токам различных гармоник.
4. Расчёт комплексных сопротивлений всех ветвей электрической цепи для каждой из гармоник (см. 5.8.1). · Сопротивление ветвей постоянному току
Z 1(0) = - j XC2(0) + R1 = ∞ + 11 = ∞ Ом, то есть для постоянного тока эта ветвь представляет разрыв и может не учитываться в расчётах. Z 2(0) = R2 + jXL1(0) = 15 + j0 = 15 Ом,
то есть для постоянного тока эта ветвь представляет собой только резистор R2 .
Z 3(0) = R3 = 48 Ом.
· Сопротивление ветвей первой гармонике тока.
Z 1(1) = - j XC2(1) + R1 = - j11,45 + 11 = 15,88 e – j46,15 Ом.
Z 2(1) = R2 + jXL1(1) = 15 + j64 = 65,7 e j 76,8 Ом,
Z 3(1) = R3 = 48 Ом
· Сопротивление ветвей третьей гармонике тока.
Z 1(3) = - j XC2(3) + R1 = - j3,82+ 11 = 11,6 e – j 19,1 Ом.
Z 2(3) = R2 + jXL1(3) = 15 + j192 = 192,6 e j 86,2 Ом,
Z 3(3) = R3 = 38 Ом
5. Расчёт токов во всех ветвях и общего тока первоначально проводим в комплексной форме по отдельным гармоникам. Для постоянной составляющей тока схема электрической цепи имеет вид (рис. 6.7).
Рис. 6.7. Схема замещения электрической цепи для токов от постоянной составляющей напряжения
I2(0) =
I3(0) =
По первому закону Кирхгофа входной ток I(0) определяется как сумматоков ветвей (см. 5.7.2). I(0) = I2(0) + I3(0) = 3,3 + 1,04 = 4,34 А.
Для первой гармоники тока схема электрической цепи имеет вид (рис. 6.8).
Рис. 6.8. Схема замещения электрической цепи для токов от первой гармоники напряжения
В связи с тем, что первая гармоника напряжения имеет синусоидальный характер, расчёт необходимо вести в комплексной форме. При этом удобнее рассчитывать в комплексах амплитудного, а не действующего значения, чтобы сначала не делить, а потом не умножать на Мгновенному значению первой гармоники напряжения соответствует комплекс амплитудного значения первой гармоники (см. 5.3).
Тогда токи в трёх ветвях электрической цепи определятся как одинаковое для всех их напряжение, делённое на комплексное сопротивление ветви первой гармонике тока.
Ỉ1m(1) =
= 20,15(cos(73,150 ) + jsin(73,150 )) = 5,84 + j19,28 А;
Ỉ2m(1) = + jsin(– 49,80 )) = 3,14 – j3,72 А;
Ỉ3m(1)= = 7,5 + j3,8 = А.
Общий ток трёх ветвей находится по первому закону Кирхгофа как сумма рассчитанных токов.
Ỉm(1) = Ỉ1m(1) + Ỉ2m(1) + Ỉ3m(1) = 5,84 + j19,28 + 3,14 – j3,72 + 7,5 + j3,8 =
= 16,48 + j19,36 = 25,42 е j49,6
Комплексам амплитудного значения рассчитанных токов соответствуют следующие их мгновенные значения.
i 1(1 ) = 20,15 sin(502t + 73,150) А;
i 2(1) = 4,87 sin(502t – 49,80) А;
i 3(1) = 8,42 sin(502t + 270) А;
i (1) = 25,42 sin(502t + 49,60) А.
Для третьей гармоники схема замещения будет иметь тот же вид (рис. 6.7), но сопротивления ветвей будут другими в связи с отличающимися сопротивлениями катушки индуктивности и конденсатора токам утроенной частоты. Мгновенному значению третьей гармоники напряжения соответствует комплекс амплитудного значения третьей гармоники.
Ỉ1m(3) = = 3,9 + j7,69 А;
Ỉ2m(3) = + jsin(– 42,20 )) = 0,39 – j0,35 А;
Ỉ3m(3)= J1,83 А.
Общий ток трёх ветвей находится по первому закону Кирхгофа как сумма рассчитанных токов.
Ỉm(3) = Ỉ1m(3) + Ỉ2m(3) + Ỉ3m(3) = 3,9 + j7,69 + 0,39 – j0,35 + 1,89 + j1,83 = = 6,18 + j9,17= 11,06 е j56.
Комплексам амплитудного значения рассчитанных токов третьей гармоники соответствуют следующие их мгновенные значения.
i 1(3 ) = 8,62 sin(1506t + 63,10) А;
i 2(3) = 0,52 sin(1506t – 42,20) А;
i 3(3) = 2,63 sin(1506t + 440) А;
i (3) = 11,06 sin(1506t + 560) А.
В целом мгновенные значения всех токов определяются суммой их гармонических составляющих (см. 5.6).
i 1(t) = i 1(1 ) + i 1(3 ) = 20,15 sin(502t + 73,150) + 8,62 sin(1506t + 63,10) А;
i 2(t) = I2(0) + i 2(1) + i 2(3) = 3,3+4,87 sin(502t – 49,80) +0,52 sin(1506t– 42,20) А;
i 3(t) = I3(0) + i 3(1) + i 3(3) =1,04+ 8,42 sin(502t + 270) +2,63 sin(1506t + 440) А;
i(t) = I(0)+ i (1 )+ i (3) = 4,34 + 25,42 sin(502t + 49,60) + 11,06 sin(1506t + 560) А.
6. Для построения графиков мгновенных значений напряжения u(t) и входного тока i(t) используются их выражения.
u(t) = 50 + 320 sin(502t + 270) + 100 sin(1506t + 440) В;
i(t) = 4,34 + 25,42 sin(502t + 49,60) +11,06 sin(1506t+ 560) А. При построении графиков необходимо определить период первой гармоники, которое задаётся как отрезок времени для кривых напряжения и тока и в течение которого можно наиболее полно проследить их изменение во времени. Т(1) = 1: f(1) = 1: 80 = 0,0125 с.
Рационально строить кривые с помощью компьютера. При этом надо перевести начальную фазу в радианы. То есть выражения для напряжения и тока примут вид.
u(t) = 50 + 320 sin(502t + 27• π;:180) + 100 sin(1506t + 44• π: ( 3•180)) В;
i(t) = 4,34 + 25,42 sin(502t + 49,6• π;:180) +11,06 sin(1506t+ 56• π: ( 3•180)) А.
Графики мгновенных значений напряжения и тока представлены на рис. 6.8.
Рис. 6.8. Графики мгновенных значений напряжения и тока.
7. Расчёт показаний амперметра и вольтметра электромагнитной и ваттметра электродинамической системы. Приборы электромагнитной системы измеряют действующее значение токов и напряжений.
|



 Ом.
Ом. Ом.
Ом.
 Поскольку при параллельном соединении ко всем ветвям приложено одно и то же напряжение, то токи в них определяются по формулам.
Поскольку при параллельном соединении ко всем ветвям приложено одно и то же напряжение, то токи в них определяются по формулам.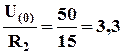 A.
A. A.
A.
 .
. u1 (t) = 320 sin(502t + 270) Ủm(1) = 320 e j 27
u1 (t) = 320 sin(502t + 270) Ủm(1) = 320 e j 27
 4,87(cos(– 49,80 ) +
4,87(cos(– 49,80 ) +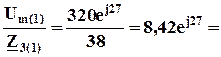 8,42((cos(270 ) + jsin(270 )) =
8,42((cos(270 ) + jsin(270 )) = 8,62(cos(63,10 ) + jsin(63,10 )) =
8,62(cos(63,10 ) + jsin(63,10 )) = 0,52(cos(– 42,20 ) +
0,52(cos(– 42,20 ) + 2,63((cos(440 ) + jsin(440 )) =
2,63((cos(440 ) + jsin(440 )) =



