Виды нагрузок по продолжительности действия (перечислить и дать примеры по каждому виду).
1. Постоянные - вес зданий и сооруж., вес и давление грунтов, горное давление, усилие от предварительного напряжения. 2. Временные длительные – вес стационарного оборудования, вес складов, хранилищ, вес и давление жидкостей, газов сыпучих материалов в ёмкостях и трубопроводах, вес воды на плоских покрытиях, отложения технологической пыли. 3. Кратковременные – действие непостоянно, кратковременные нагрузки, нагрузки перекрытий жилых и общественных зданий, атмосферные нагрузки, температурные воздействия, технологические факторы. 4. Особые – могут появляться в исключительных случаях – взрывные воздействия, сейсмические воздействия, нагрузки при аварии технологического процесса, просадка грунтов. 1.31Как определяются атмосферные нагрузки (снеговая и ветровая). а) снеговая Нормативное значение СН на 1м2 перекрытия определяется: ρ=ρX*μ ρX – нормативная нагрузка на 1м2 при α≤25° – μ=1 при α≥60° – μ=0 α- угол наклона кровли (покрытия) б) ветровая Состоит из среднестатистической и пульсационной. Нормативное значение средней сост. ветровой нагрузки Um=ω0*k*c ω0 – нормативное значение ветрового давления принимаемая в зависимости от района строительства. k – коэффициент, учитывающий возрастание скоростного напора ветра по высоте. с - аэродинамический коэффициент 1.32 Записать условие расчета по второй группе предельных состояний. В чем особенность этого расчета?
fn – нормативный прогиб f – расчётный прогиб Ограничение максимального прогиба.
Блок 2 Расчет сжатых элементов на прочность. Привести расчетные формулы и раскрыть их содержание. Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой
N- продольная сила;
Расчет на прочность растянутых элементов конструкций из стали с отношением
Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой
Значения
2.3Расчет изгибаемых элементов в упругой стадии (проиллюстрировать эпюрой напряжений, привести расчетные формулы и раскрыть их содержание).
l1=2/3∙h M1=(b∙h2/6)∙σy=W1∙σy Расчет на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле
Значения касательных напряжений
При наличии ослабления стенки отверстиями для болтов значения
где Для расчета на прочность стенки балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, следует определять местное напряжение
где
где Так же следует проверять на совместность действия нормальный и касательных напряжений (Вроде как это для балок стенок, но про это лучше не писать, промолчатьJ):
Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки, следует выполнять по формуле
где
Устойчивость балок не следует проверять: -при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (железобетонные плиты, плоский и профилированный металлический настил, волнистая сталь и т.п.); -при отношении расчетной длины балки Расчет изгибаемых элементов в упруго-пластической стадии (проиллюстрировать эпюрами напряжений, привести расчетные формулы и раскрыть их содержание). Весь расчет делается по двум стадиям – первая, упругая (появление фибровой текучести), вторая, пластическая(пластические деформации пронизывают всё сечение). Условие пластичности. Установлено, что при
Рис.6.1.. Идеализированная диаграмма работы пластичной стали При одноосном напряжённом состоянии переход в пластическую стадию происходит при достижении нормальным напряжением предела текучести. При многоосном напряжённом состоянии переход в пластическую стадию зависит не от одного напряжения, а от функции напряжений, характеризующих условия пластичности. Работе стали и алюминиевых сплавов наиболее близки третья и четвертая теории прочности. В СНиП принята четвертая, энергетическая теория прочности. По этой теории пластичность наступает тогда, когда работа изменения формы тела достигает наибольшей величины. С учетом пластических деформаций:
LII=h/2 MII=ДIIlII=(b∙h2)/4∙σy=WII∙σy C=MII/MI Wpl=WII при изгибе в одной из главных плоскостей при касательных напряжениях
при изгибе в двух главных плоскостях при касательных напряжениях
здесь
Расчет в опорном сечении балок (при
При наличии зоны чистого изгиба в формулах (39) и (40) вместо коэффициентов
При одновременном действии в сечении момента при при где здесь
С целью оптимизации балок при их расчете с учетом требований пп. 5.20, 7.5, 7.24 и 13.1 значения коэффициентов При наличии ослабления стенки отверстиями для болтов значения касательных напряжений 2.5 Что такое шарнир пластичности при изгибе балки? Показать эпюру нормальных напряжений, отвечающих появлению шарнира пластичности. Как определяется пластический момент сопротивления для любого сечения?). Переход материала в упруго – пластическую стадию при сдвиге. Шарнир пластичности. После исчерпания упругой работы в сплошных изгибаемых элементах, выполненных из пластичных сталей, пластические деформации распространяются в глубь сечения (рис.) и в предельном состоянии пронизывают все сечение, образуя так называемый «шарнир пластичности».
При развитии пластических деформаций прогибы так же быстро растут, а при образовании шарнира пластичности прогибы растут беспредельно. Эпюра напряжений такого состояния имеет вид двух прямоугольников с ординатами из двух прямоугольников. Тогда предельный момент внутренних сил определяется из выражения
В упругой стадии С учётом развития пластических деформаций условие прочности имеет вид:
где Wpl=C1´Wx или Пример: доказать, что для прямоугольного сечения С1=1,5.
С1= 2.6 При выполнении каких условий, допускается рассчитывать изгибаемые элементы по упруго-пластической стадии (для разрезных и неразрезных балок).(Дополнить Img49) I) Расчет на прочность по упруго-пластической стадии допускается для изгибаемых разрезных балок сплошного сечения из стали с пределом текучести до 530 МПа (5400 кгс/кв.см), несущих статическую нагрузку, при соблюдении: 1) Расчет на прочность балок переменного сечения с учетом развития пластических деформаций следует выполнять только для одного сечения с наиболее неблагоприятным сочетанием усилий 2) Для обеспечения общей устойчивости балок, рассчитываемых с учетом развития пластических деформаций, необходимо, чтобы либо были выполнены требования п. 5.16*, 3) В балках, рассчитываемых с учетом развития пластических деформаций, стенки следует укреплять поперечными ребрами жесткости согласно требованиям пп. 7.10, 7.12 и 7.13, в том числе в местах приложения сосредоточенной нагрузки. 4) Расчет на устойчивость стенок балок симметричного сечения с учетом развития пластических деформаций при отсутствии местного напряжения (
где
здесь 5) В изгибаемых элементах отношение ширины свеса сжатого пояса II) Расчет на прочность по упруго-пластической стадии допускается для неразрезных и защемленных балок постоянного двутаврового сечения, изгибаемых в плоскости наибольшей жесткости, со смежными пролетами, отличающимися не более чем на 20 %, несущих статическую нагрузку, при условии соблюдения требований (с учетом перераспределения опорных и пролетных моментов): 1) Для обеспечения общей устойчивости балок, рассчитываемых с учетом развития пластических деформаций, необходимо, чтобы либо были выполнены требования п. 5.16*, 2) В балках, рассчитываемых с учетом развития пластических деформаций, стенки следует укреплять поперечными ребрами жесткости согласно требованиям пп. 7.10, 7.12 и 7.13, в том числе в местах приложения сосредоточенной нагрузки. 3) Расчет на устойчивость стенок балок симметричного сечения с учетом развития пластических деформаций при отсутствии местного напряжения (
где
здесь 4) В изгибаемых элементах отношение ширины свеса сжатого пояса Расчетные значения изгибающего момента
где
здесь а) в неразрезных балках со свободно опертыми концами большему из значений
где символ
б) в однопролетных и неразрезных балках с защемленными концами в) в балке с одним защемленным и другим свободно опертым концом значение Расчетное значение поперечной силы 2.7 Расчет элементов на прочность в упругой стадии при действии изгибающих моментов в двух плоскостях (привести расчетные формулы и раскрыть их содержание). Расчет на прочность элементов, изгибаемых в двух главных плоскостях, следует выполнять по формуле
Если tgα ≤ 0.25 – ставится 1 тяж. Если tgα >0.25 – ставится 2 тяжа. В балках, изгибаемых в двух плоскостях, значения напряжений в стенке балки должны быть проверены по следующим формулам в двух главных плоскостях изгиба.
При выполнении следующего требования проверка устойчивости балок, изгибаемых в двух плоскостях, не требуется: при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (плиты железобетонные из тяжелого, легкого и ячеистого бетона, плоский и профилированный металлический настил, волнистую сталь и т. п.); Расчет элементов на прочность в упруго-пластической стадии при действии изгибающих моментов в двух плоскостях (привести расчетные формулы и раскрыть их содержание). Весь расчет делается по двум стадиям – первая, упругая (см. предыдущий вопрос), вторая, пластическая. при изгибе в двух главных плоскостях при касательных напряжениях
здесь
Расчет в опорном сечении балок (при
При наличии зоны чистого изгиба в формулах (39) и (40) вместо коэффициентов
При одновременном действии в сечении момента при при где здесь
С целью оптимизации балок при их расчете с учетом требований пп. 5.20, 7.5, 7.24 и 13.1 значения коэффициентов При наличии ослабления стенки отверстиями для болтов значения касательных напряжений
|

 =
= 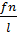
 , следует выполнять по формуле
, следует выполнять по формуле
 - площадь сечения нетто;
- площадь сечения нетто; - расчетное сопротивление стали растяжению, сжатию, изгибу по пределу текучести;
- расчетное сопротивление стали растяжению, сжатию, изгибу по пределу текучести; - коэффициент условий работы;
- коэффициент условий работы; >
>  , эксплуатация которых возможна и после достижения металлом предела текучести, следует выполнять по формуле
, эксплуатация которых возможна и после достижения металлом предела текучести, следует выполнять по формуле
 - расчетное сопротивление стали растяжению, сжатию, изгибу по временному сопротивлению;
- расчетное сопротивление стали растяжению, сжатию, изгибу по временному сопротивлению; - коэффициент надежности в расчетах по временному сопротивлению;
- коэффициент надежности в расчетах по временному сопротивлению; .
. - площадь сечения брутто;
- площадь сечения брутто; - коэффициент продольного изгиба;
- коэффициент продольного изгиба; следует определять по СНиП в зависимости от гибкости
следует определять по СНиП в зависимости от гибкости  .
. ;
;  ;
;  ;
; 
 Д1=Z1=0.5∙(h/2)∙σy∙b
Д1=Z1=0.5∙(h/2)∙σy∙b .
. - момент, изгибающий момент;
- момент, изгибающий момент; - моменты сопротивления сечения нетто относительно осей соответственно
- моменты сопротивления сечения нетто относительно осей соответственно  и
и 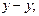 (min-минимальный для данного сечения)
(min-минимальный для данного сечения) в сечениях изгибаемых элементов должны удовлетворять условию
в сечениях изгибаемых элементов должны удовлетворять условию
 - расчетное сопротивление стали сдвигу;
- расчетное сопротивление стали сдвигу; - поперечная сила, сила сдвига;
- поперечная сила, сила сдвига; - статический момент сдвигаемой части сечения брутто относительно нейтральной оси;
- статический момент сдвигаемой части сечения брутто относительно нейтральной оси; - моменты инерции сечения брутто относительно осей соответственно
- моменты инерции сечения брутто относительно осей соответственно  - толщина;
- толщина; , определяемый по формуле
, определяемый по формуле ,
, - шаг отверстий;
- шаг отверстий;  - диаметр отверстия.
- диаметр отверстия. по формуле
по формуле ,
, - расчетное значение нагрузки (силы);
- расчетное значение нагрузки (силы); - условная длина распределения нагрузки, определяемая в зависимости от условий опирания; например, для опирания на верхний пояс
- условная длина распределения нагрузки, определяемая в зависимости от условий опирания; например, для опирания на верхний пояс ,
,
 - толщина верхнего пояса балки.
- толщина верхнего пояса балки.
 ,
, - следует определять для сжатого пояса;
- следует определять для сжатого пояса; - коэффициент снижения расчетных сопротивлений при изгибно-крутильной форме потери устойчивости балок;(следует определять согласно СНиП.)
- коэффициент снижения расчетных сопротивлений при изгибно-крутильной форме потери устойчивости балок;(следует определять согласно СНиП.) , не превышающим значений, определяемых табличными формулами СНиП.
, не превышающим значений, определяемых табличными формулами СНиП. после упругой работы и небольшого переходного участка наступает пластическое течение, что на диаграмме отмечается протяжённой площадкой текучести. В целях упрощения расчётных предпосылок при работе конструкции в упруго – пластической стадии диаграмма работы стали уподоблена работе идеального упругого тела, которое совершенно упруго до предела текучести и совершенно пластично после него (рис., диаграмма Прандтля).
после упругой работы и небольшого переходного участка наступает пластическое течение, что на диаграмме отмечается протяжённой площадкой текучести. В целях упрощения расчётных предпосылок при работе конструкции в упруго – пластической стадии диаграмма работы стали уподоблена работе идеального упругого тела, которое совершенно упруго до предела текучести и совершенно пластично после него (рис., диаграмма Прандтля).
 ДII=ZII=(h/2)∙σy∙b
ДII=ZII=(h/2)∙σy∙b 0,9
0,9  (кроме опорных сечений)
(кроме опорных сечений) (39)
(39) 0,5
0,5  (кроме опорных сечений)
(кроме опорных сечений) (40)
(40) и
и  - абсолютные значения изгибающих моментов;
- абсолютные значения изгибающих моментов; - коэффициент, определяемый по формулам (42) и (43);
- коэффициент, определяемый по формулам (42) и (43); и
и  - коэффициенты, принимаемые по табл. 66.
- коэффициенты, принимаемые по табл. 66. 0;
0;  0 и
0 и  0) следует выполнять по формуле
0) следует выполнять по формуле (41)
(41) и
и 
 следует определять по формулам:
следует определять по формулам: (42)
(42)

 ; (44)
; (44) - коэффициент, принимаемый по табл. 66;
- коэффициент, принимаемый по табл. 66; - соответственно толщина и высота стенки;
- соответственно толщина и высота стенки; - коэффициент, равный
- коэффициент, равный  0 - для других типов сечений;
0 - для других типов сечений;
 и
и  в формулах (39) и (40) допускается принимать меньше значений, приведенных в табл. 66, но не менее 1,0.
в формулах (39) и (40) допускается принимать меньше значений, приведенных в табл. 66, но не менее 1,0.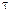 следует умножать на коэффициент, определяемый по формуле (30).
следует умножать на коэффициент, определяемый по формуле (30). Рис. 6.2. Работа изгибаемого элемента под нагрузкой
Рис. 6.2. Работа изгибаемого элемента под нагрузкой ,
,  ,
,
 ,
, .
.
 ; Sx для отсечённой (заштрихованной) части:
; Sx для отсечённой (заштрихованной) части: 
 в остальных сечениях учитывать развитие пластических деформаций не допускается.Расчет на прочность изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/кв.см), воспринимающих динамические, вибрационные или подвижные нагрузки, допускается выполнять с учетом развития пластических деформаций, не препятствующих требуемым условиям эксплуатации конструкций и оборудования.
в остальных сечениях учитывать развитие пластических деформаций не допускается.Расчет на прочность изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/кв.см), воспринимающих динамические, вибрационные или подвижные нагрузки, допускается выполнять с учетом развития пластических деформаций, не препятствующих требуемым условиям эксплуатации конструкций и оборудования. , либо наибольшие значения отношений расчетной длины балки к ширине сжатого пояса
, либо наибольшие значения отношений расчетной длины балки к ширине сжатого пояса 
 определяемые по формулам табл. 8*, были уменьшены умножением на коэффициент
определяемые по формулам табл. 8*, были уменьшены умножением на коэффициент  здесь
здесь  Учет пластичности при расчете балок со сжатым поясом менее развитым, чем растянутый, допускается лишь при выполнении условий п. 5.16*,
Учет пластичности при расчете балок со сжатым поясом менее развитым, чем растянутый, допускается лишь при выполнении условий п. 5.16*,  0) и при
0) и при  0,9
0,9 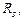
 0,25, 2,2
0,25, 2,2  6 следует выполнять по формуле
6 следует выполнять по формуле

 следует принимать по табл. 6*, а
следует принимать по табл. 6*, а  - определять по формуле (73).
- определять по формуле (73). к толщине
к толщине  следует принимать не более значений, определяемых по табл. 30.
следует принимать не более значений, определяемых по табл. 30.
 здесь
здесь  Учет пластичности при расчете балок со сжатым поясом менее развитым, чем растянутый, допускается лишь при выполнении условий п. 5.16*,
Учет пластичности при расчете балок со сжатым поясом менее развитым, чем растянутый, допускается лишь при выполнении условий п. 5.16*, 

 следует определять по формуле
следует определять по формуле (45)
(45) - наибольший изгибающий момент в пролете или на опоре, определяемый из расчета неразрезной балки в предположении упругой работы материала;
- наибольший изгибающий момент в пролете или на опоре, определяемый из расчета неразрезной балки в предположении упругой работы материала; - коэффициент перераспределения моментов, определяемый по формуле
- коэффициент перераспределения моментов, определяемый по формуле (46)
(46) - условный изгибающий момент, равный:
- условный изгибающий момент, равный: (47)
(47) (48)
(48) означает, что следует найти максимум всего следующего за ним выражения;
означает, что следует найти максимум всего следующего за ним выражения; - изгибающий момент в крайнем пролете, вычисленный как в свободно опертой однопролетной балке;
- изгибающий момент в крайнем пролете, вычисленный как в свободно опертой однопролетной балке; - максимальный изгибающий момент в промежуточном пролете, вычисленный как в свободно опертой однопролетной балке;
- максимальный изгибающий момент в промежуточном пролете, вычисленный как в свободно опертой однопролетной балке; до крайней опоры;
до крайней опоры; - длина крайнего пролета;
- длина крайнего пролета; 0,5
0,5  , где
, где  - наибольший из моментов, вычисленных как в балках с шарнирами на опорах;
- наибольший из моментов, вычисленных как в балках с шарнирами на опорах; в формуле (44) следует принимать в месте действия
в формуле (44) следует принимать в месте действия  . Если
. Если  - момент в пролете, следует проверить опорное сечение балки.
- момент в пролете, следует проверить опорное сечение балки.







 (40)
(40) и
и  - абсолютные значения изгибающих моментов;
- абсолютные значения изгибающих моментов; - коэффициент, определяемый по формулам (42) и (43);
- коэффициент, определяемый по формулам (42) и (43); и
и  0 и
0 и  (41)
(41) и
и 
 коэффициент
коэффициент  следует определять по формулам:
следует определять по формулам: (42)
(42)

 ; (44)
; (44) - коэффициент, принимаемый по табл. 66;
- коэффициент, принимаемый по табл. 66; - соответственно толщина и высота стенки;
- соответственно толщина и высота стенки;
 и
и 


