Проверка прочности изгибаемых элементов при совместном действии нормальных и касательных напряжений.
При совместном действии изгибающего момента и поперечной силы условие образования шарнира пластичности определяется некоторой функцией, имеющей достаточно громоздкие вычисления. Поэтому для упрощения расчета, с достаточной точностью вычислений (с небольшим запасом), согласно СНиП II-23-81*, распространение пластических деформаций по стенке учитывают эквивалентным повышение расчетного сопротивления на 15%. В общем случае приведенные напряжения в стенке балок при действии нормальных напряжений в двух направлениях
При этом каждое из напряжений не должно превышать расчетного сопротивления, т.е.:
где Для разрезных балок дальнейшее увеличение нагрузки невозможно, т.к. наступает предельное состояние первой группы (по несущей способности и непригодности к эксплуатации) вследствие чрезмерного развития пластических деформаций. Для неразрезных балок образование шарнира пластичности приводит к перераспределению моментов и понижению степени статической неопределимости конструкции.
2.10(11) Расчет внецентренно-сжатых элементов, на прочность в упругой и упруго-пластической стадиях (проиллюстрировать эпюрами напряжений, привести расчетные формулы и объяснить входящие в них величины). Внецентренно растянутые и короткие внецентренно сжатые элементы проверяются на прочность, а длинные – на устойчивость. Ryn стремится к 530 МПа, при любых видах нагрузок и при динамических нагрузках проверяется расчетом на прочность
где Изгибаемые элементы при статической нагрузке следует рассчитывать с учетом пластических деформаций и образования шарниров пластичности:
где
2.12По каким формулам определяются, напряжения при свободном кручении? Объяснить входящие в формулы величины.
Мк-крутящий момент, r-расстояние от центра кручения до точки в которой касательные напряжения имеют моксимальные значения. Ik-момент инерции при кручении Ik=α(Ik1+ Ik2+ Ik3+… +Ikn) α-коэффициент:для двутавров-1.3 2.13По каким формулам определяются напряжения при стесненном кручений? Объяснить входящие в формулы величины.
w1=∫А w2dA w1-секториальная площадь крайней точки сечения В-бимомент, В= Мп*h, h -расстояние между моментами Расчет сжатых элементов на общую устойчивость (привести расчетные формулы и раскрыть их содержание).
где А – площадь; f - определяется по СниП в зависимости от условной гибкости Эта условная гибкость определяется как:
i - радиус инерции А – площадь; I – момент инерции. lef = lc m, где lc – длина стойки; m - коэффициент приведения, т.е. расчетная длина зависит от условий закрепления. Например, с шарнирно опертыми стойками m = 1. 2.15 Привести значение критической силы для центрально-сжатого стержня, Показать графически взаимосвязь бcr с гибкостью стержня Лямда. Как по СНиП определяется Фи? Ncr= π2EI/lef2 lef- расчетная длина стержня EI-жесткость стержня f=π2E/l* Зная знаение l и марку стали определяем f +диаграмма Расчет на устойчивость внецентренно-сжатых элементов в плоскости действия изгибающего момента (привести расчетную зависимость и раскрыть ее содержание).
fe-коэффициент снижения расчетных сопротивлений при внецентренном сжатии
ɣc-к-т условий работы ɣn-к-т надежности по назначению N-продольная сила Расчет на устойчивость внецентренно-сжатых элементов в плоскости, перпендикулярной плоскости действия изгибающего момента (привести расчетную зависимость, и раскрыть ее содержание).
fy-коэффициент продольного изгиба
ɣc-к-т условий работы ɣn-к-т надежности по назначению N-продольная сила С-к-т для расчета на прочность с учетом развития пластических деформаций при изгибе 2.18 Как определяется e m mef, Для внецентренно загруженных стержней, что это за параметры? е=M/N-ексцентриситет m=е/ρх-относительный ексцентриситет mef= m*ɧ-относительный приведенный ексцентриситет ɧ-к-т влияния формы сечения 2.19Написать выражения: гибкости, условной гибкости, расчетной длины. Гибкость определяется по формуле: l = lef/i; i - радиус инерции; lef – расчетная длина стержня;
условная гибкость определяется как:
lef = lc m, где lc – длина стойки; m - коэффициент приведения, т.е. расчетная длина зависит от условий закрепления. Например, с шарнирно опертыми стойками m = 1.
2.20 Объясните величины Фи Фие, Фиb. От каких параметров зависит каждая из них? Определение Фи и Фие по СНиП f-коэффициент продольного изгиба l = lef/i,i - радиус инерции, lef – расчетная длина стержня; lef = lc m, где lc – длина стойки; m - коэффициент приведения, т.е. расчетная длина зависит от условий закрепления. Например, с шарнирно опертыми стойками m = 1.
Зная значение l и марку стали определяем f fе-коэффициент снижения расчетных сопротивлений при внецентренном сжатии(принимается в зависимости от условной гибкости fb-коэффициент снижения расчетных сопротивлений при изгибно- крутильной крутильной форме потери устойчивости(определяется по приложению 7 СНиП) 2.21 Расчет На общую. устойчивость изгибаемых элементов (привести расчетную зависимость и объяснить входящие в нее величины). Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки, следует выполнять по формуле
где
ɣc-к-т условий работы
2.22 В каких случаях не требуется проверка общей устойчивости изгибаемых элементов? Устойчивость балок не следует проверять: -при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (железобетонные плиты, плоский и профилированный металлический настил, волнистая сталь и т.п.); -при отношении расчетной длины балки 2.23. Как можно повысить общую устойчивость изгибаемых элементов? Для упругого стержня с шарнирно закрепленными концами критическая сжимающая сила определяется формулой Л. Эйлера
Соответственно критические напряжения
Формула справедлива только при постоянном модуле упругости Формула (1.2) показывает, что несущая способность стержня может быть увеличена путем увеличения момента инерции, без изменения площади поперечного сечения, путем размещения материала как можно дальше от главных осей инерции поперечного сечения. Поэтому трубчатые сечения наиболее экономичны, чем сплошные сечения. Уменьшая толщину стенки таких сечений и увеличивая поперечные размеры, можно повысить их устойчивость. Эти рассуждения показывают, что устойчивость упругих систем или боковое выпучивание сжатых элементов имеет большое практическое значение. Это особенно справедливо во многих новейших конструкциях, в которых размеры поперечного сечения делаются все меньшими и меньшими благодаря использованию прочных материалов в целях экономии веса. Во многих случаях разрушение инженерных сооружений объясняется упругой неустойчивостью, а не недостаточной прочностью материала. При опытных исследованиях явления выпучивания сжатых стержней установлено, что связь между прогибом и нагрузкой зависит в значительной степени от точности, с какой центрирована нагрузка, и от прямизны и однородности стержня. Расчет элементов сечения на местную устойчивость (при действии нормальных напряжений, касательных, а также при совместном действии нормальных и касательных напряжений). Основные мероприятия по обеспечению местной устойчивости полки и стенки двутавровой балки. Нормальных σкр=скр*R/λ2ст Касательных τ=10,3*Rcр/λ-2ст Совместное Варируя размерами пластинки и условиями закрепления добиваемся повышения σкр
|

 и
и  и касательных напряжений
и касательных напряжений 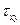 проверяют по формуле
проверяют по формуле – в одной плоскости
– в одной плоскости ;
;  ;
;  ,
, - нормальное напряжение, параллельное оси балки;
- нормальное напряжение, параллельное оси балки;  - касательное напряжение;
- касательное напряжение;  - толщина стенки;
- толщина стенки;  - статический момент отсеченной части.
- статический момент отсеченной части. - в двух плоскостях
- в двух плоскостях - в трех плоскостях.
- в трех плоскостях. =
= 
 и
и  - координаты рассматриваемой точки сечения относительно его главных осей.
- координаты рассматриваемой точки сечения относительно его главных осей. (49)
(49) и
и  - абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании;
- абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании; и
и  - коэффициенты, принимаемые по прил. 5.
- коэффициенты, принимаемые по прил. 5.
 =Мк*r/Ik
=Мк*r/Ik =В/
=В/ 

 .
. , где l - гибкость, т.е. l = lef/i; E – модуль упругости;
, где l - гибкость, т.е. l = lef/i; E – модуль упругости; ; lef – расчетная длина стержня;
; lef – расчетная длина стержня; т.е. l = lef/i,i - радиус инерции, lef – расчетная длина стержня;
т.е. l = lef/i,i - радиус инерции, lef – расчетная длина стержня;

 ,
, - следует определять для сжатого пояса;
- следует определять для сжатого пояса;  - следует определять согласно СНиП.
- следует определять согласно СНиП. к ширине сжатого пояса
к ширине сжатого пояса  , не превышающим значений, определяемых табличными формулами СНиП.
, не превышающим значений, определяемых табличными формулами СНиП. . (1.1)
. (1.1)

 (1.2)
(1.2) , в пределах упругих деформаций, т.е. при напряжениях, не превышающих предел пропорциональности, и
, в пределах упругих деформаций, т.е. при напряжениях, не превышающих предел пропорциональности, и 
 . При средних и малых гибкостях стержня потеря его устойчивости происходит в упругопластической стадии работы материала при
. При средних и малых гибкостях стержня потеря его устойчивости происходит в упругопластической стадии работы материала при  <
<  <
<  .
.



