Информация как преобразование в процессе управления
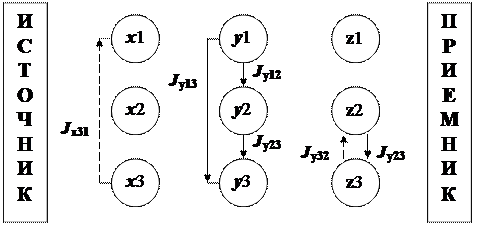
Все понятия, определённые для преобразований в раздел 1.3, можно применить также к поперечным множествам сообщений цепи управления. Информационная ассоциация – это ассоциация, состоящая из сообщений поперечного множества. В цепи управления, изображённой на рис. 1.8., информационными ассоциациями являются, например, следующие: { x 1, x 2 }, { y 1, y 2 }, { z1, z2 } и т.п.
Рис. 1.8. Информации в цепи управления
Информация – это преобразование одного сообщения информационной ассоциации в другое сообщение той же ассоциации. Обозначать информации будем символом J с индексами, указывающими на первичное и вторичное сообщения, т.е. на направление и место действия этих преобразований. На рис. 1.8. стрелками отмечены некоторые информации данной цепи управления. Из определения следует, что информацияхарактеризует пару сообщений из поперечного их множества как преобразование, которому следует подвергнуть одно сообщение этой пары (ассоциации), чтобы получить другое сообщение той же пары. В этом смысле можно говорить, что пара сообщений – информационная ассоциация – содержит информацию. Нетривиальнаяинформация – это информация, соответствующая нетривиальному преобразованию. Аналогично этому определяются следующие информации: тривиальная, тождественная, равнозначная, информация, обратная данной информации, операционная, обратная операционная, основная, обратная основной, ассоциационная информация. Например, информация, обратная к данной – обратнаяинформация – это информация, соответствующая такому преобразовании, применение которого ко вторичному сообщению даёт первичное сообщение той же ассоциации. Тривиальная информация содержится в ассоциации неразличимых сообщений. При этом тождественность или одинаковость сообщений на практике является следствием их неразличимости, откуда вытекает, что число разных информации, содержащихся во множествах сообщений, определяется не только реальными фактами, но и разрешающей способностью приёмника, т.е. получаемая информация может быть в определённой степени субъективна. Равнозначная информация подучается, например, когда последовательно наблюдаются два неразличимых предмета (например, два последовательных кинокадра с одним и тем же изображением). Тождественная информация получается, когда последовательно наблюдается один и тот же предмет (например, одна и та же фотография). Информационная цепь – это цепь, образованная из сообщений поперечного множества сообщений. На рис. 1.8. информационная цепь образована, например, упорядоченным множеством сообщений < x 1, x 2, x 3 >. В зависимости от места расположения в цепи управления можно различать цепь оригиналов, цепь сообщений и цепь образов. С формальной точки зрения очерёдность сообщений в информационной цепи может быть произвольной. Однако для правильного информирования в процессе управления необходимо, чтобы в различных поперечных множествах сообщений одной и той же цепи управления (в цепи оригиналов, в цепях промежуточных сообщений и цепи образов) соблюдался один и тот же порядок, т.е. сообщения разных информационных цепей в определённой цепи управления должны быть упорядочены одинаково. Например, порядок действия операций в решаемом уравнении должен соответствовать последовательности операций в программе для ЦВМ и тот же порядок должен быть при их выполнении; последовательность реальных событий должна соответствовать последовательности изображений на кадрах кинохроники и т.п. Употребление на практике общепринятых определённых способов упорядочения сообщений в информационных цепях, например, по времени и по направлению движения, диктуется соображениями удобства их использования. Такое упорядочение применяется, например, при построчной передаче телевизионного изображения. Заметим, что определённые способы упорядочения, существующие в природе, а также, возможно, общепринятые людьми, являются такими и именно такими, т.к. подчиняются неизвестным пока законам организации и упорядочения элементов в сложных системах. Результирующая информация – это результирующее преобразование последовательных информаций в информационной цепи. На рис. 1.8, например, в информационной цепи < y 1, y 2, y 3 > имеются информации y 1 J y12 y 2 и y 2 J y23 y 3, для которых результирующей информацией будет y 1 J y12 J y23 y 3 или, иначе J y23 J y12 y 1 = y 3. Для информации, как и для кодов, имеют место и легко доказываются теоремы, аналогичные теоремам 1.2 и 1.3, существующим для преобразований. Теорема 1.6. В информационной цепи информация, состоящая в преобразовании первого сообщения в последнее, является результирующей информацией последовательных информации. Например, для информационной цепи промежуточных сообщений, представленной на рис. 1.8, справедливо равенство:
J y13 y 1 = J y23 J y12 y 1 . На практике утверждение теоремы 1.6 важно в тех случаях, когда при отыскании информации, содержащихся в множестве сообщений, некоторые из них можно получить из оставшихся (известных) информации, как их результирующую. Например, если напряжение во второй точке схемы на 10 В больше, чем в первой точке, а в третьей точке схемы на 27 В больше, чем во второй, то нам без дополнительного измерения известно, что напряжение в третьей точке схемы на 37 В больше, чем в первой. Теорема 1.7. Результирующая информация двух информаций, из которых одна обратна другой, является тривиальной информацией. Практическое значение этой теоремы состоит в том, что если после определенного изменения наступило обратное изменение, то полученное состояние не отличается от исходного, в силу чего нет возможности получить какую-либо информацию о происшедшем. Этим пользуется, например, чаще нерадивый школьник, когда стирает в дневнике отметку, не удовлетворяющую его родителей. Рассмотрим операционные информации, их роль в процессе управления и пользование ими. При измерениях преимущественно используются операционные информации, в которых родом операции является умножение, а параметром – число, показывающее во сколько раз измеренная величина больше единицы измерения. В обратной к данной операционной информации род операции – умножение, параметр операции – число, показывающее, во сколько раз единица измерения меньше измеренной величины. Подобная информация имеет место, например, при определении метра как 1/40 000 000 длины меридиана Земли. Операционными информациями являются изменения слов при склонении, спряжении и т.п. При этом родом операции является дописывание букв к слову, параметр – конкретные буквы или буква. В операционной информации, обратной данной, очевидно обратным родом операции является вычеркивание букв. При выражении информации языковыми средствами не всегда выделяются четыре основных элемента преобразования: первичное и вторичное сообщения, род и параметр операции. Так в односложном предложении «светает», которое, очевидно, может содержать информацию, прямо не выделены перечисленные компоненты преобразования. Однако это предложение является операционной информацией, так как здесь речь идёт о том, что положение солнца ниже горизонта становится положением солнца выше горизонта. Основнаяинформация – это операционная информация, одинаковая для всех последовательных ассоциаций информационной цепи. Если для какой-либо информационной цепи удаётся найти основную информацию или, если множество разных операционных информации становится множеством одинаковых операционных информации: J x x 1 = x 2, J x x 2 = x 3, J x x 3 = x 4 и т.д., то такую информацию всегда можно записать компактно в виде рекуррентного выражения J x x n = x n+1, в котором J х – основная информация. Например, множество членов арифметической прогрессии можно представить основной информацией вида х n + d = x n+1, в которой род операции – сложение, а параметр – d. При наличии основной информации, информация содержащаяся в информационной ассоциации, образованной от первого сообщения х 1 и некоторого n -го сообщения x n, является результирующей информацией (n - 1) последовательных основных информаций J x, т.е. J x1n x 1 = Использование основных информаций удобно потому, что, если известно хотя бы одно сообщение из множества, к которому относится основная информация, то можно найти любое сообщение данного множества. Заметим, что в математике множества описываются в соответствии с заранее заданнойосновной информацией. Например, такое алгебраическое множество элементов как «группа» образовано на одной операции – «прибавление некоторого элемента», а множество, называемое «кольцо», – на двух операциях – «прибавление и умножение некоторого элемента». Применение этих операций к любым двум элементам множества дают третий элемент того же множества. В отличие от математики, в реальной действительности основную информацию требуется отыскивать и распознавать в явлениях природы, что монет оказаться нелёгким делом. При этом в наилучшем случае поиск основной информации основывается на том, что в начале предполагается определённым род операции, после чего на основе нескольких очередных сообщений в информационной цепи определяется параметр операции, который затем проверяется во всех остальных ассоциациях. Если таким образом не удается найти основную информацию, то необходимо проделать все заново, но для другого подходящего рода операций. Ещё трудное отыскивать основную информацию, если не удаётся найти простое (однооперационное) преобразование, так как при этом приходится предполагать её более сложной, т.е. состоящей из нескольких операций. В этом случае приходится задавать n родов и (n - 1) параметров операций и на их основе искать оставшийся параметр. Таким образом, процедура поиска основной информации сводится к перебору возможных родов и параметров операций. Заметим, однако, что опыт и интуиция позволяют человеку находить основную информацию, не осуществляя полного перебора. В очень коротких информационных цепях может оказаться много основных информаций. Так зачастую малое число фактов удаётся увязать с помощью многих разных гипотез. С ростом числа сообщений в информационной цепи число основных информации уменьшается. При большом числе ассоциаций вообще может не оказаться ни одной основной информации или существует только одна. Так большое число разнородных фактов чаще не удается связать одной формулой. Распознавание и отыскание основной информации в явлениях природы, данные о которых основаны на измерениях, затруднены не только из-за возможного большого числа неизвестных родов и параметров операций. Так как измерения всегда сопряжены с погрешностями, то всегда у исследователя может возникнуть сомнение: либо расхождения экспериментальных и расчётных данных вызвано ошибками измерения, либо эти расхождения обусловлены неверным предположением об основной информации. Однако пользование основной информацией настолько удобно, что её пытаются найти хотя бы для небольших множеств сообщений или даже предпочитают иметь приближенную информацию. Такой информацией, например, является апроксимирующая зависимость для группы экспериментальных точек. Стремление получить основную информацию приводит к тому, что ее пытаются найти даже там, где её нет. Например, когда независимые данные связываются на графике такими кривыми, чтобы они имели хоть какой-нибудь «смысл». Употребление ассоциационной информации целесообразно, только когда информационная цепь состоит из одной информационной ассоциации, т.к. при этом получается информационная однозначность. Например, при пользовании таблицей квадратов легко найти в колонке квадратов число соответствующее 5 – это 25. Однако невозможно однозначно указать, какое число в первой колонке соответствует числу 5. Или, например, несомненно, что слову «да» соответствует слово «нет», чётное число – нечетному и т.п. Таким образом, при использовании ассоциационных информаций цепь управления должна быть такой, что в цепи оригиналов, в цепи образов и в цепях промежуточных сообщений должно быть только по два сообщения (рис. 1.10.). Информационной однозначностью одной информационной ассоциации можно объяснить появление двоичной единицы количества информации «бит». Каждый бит информации получается в результате выбора из двух равных множеств элементов того множества, в котором находится искомый объект. В процессе поиска выбранное множество элементов вновь делится на два равных подмножества и делается очередной выбор. Очевидно, что при каждом таком выборе имеет место лишь одна ассоциация (подмножеств), поэтому ассоциационной информации оказывается достаточно и нет необходимости привлекать операционные информации. Вопросы для закрепления и углубления материала 1. Определите информационную ассоциацию, информацию, а также перечислите и определите различные виды информации; приведите их примеры. 2. Каково влияние приёмника на определение числа информации в информационной цепи? 3. Определите информационную цепь. Какую роль в процессе управления играет определённый порядок сообщений в информационной цепи? Чем объясняется общепринятые людьми и существующие в природе определённые способы упорядочения? 4. Определите результирующую информацию и её свойства. 5. Какова роль операционных информации, основной информации? Как записывается последняя? 6. Как изменяется количество основных информации с ростом числа сообщений в информационной цепи? 7. Какова роль основных информаций в математике? 8. Почему люди стремятся отыскать основные информации? 9. Чем затруднено отыскание основной информации? 10. В каком случае возможен процесс управления с использованием ассоциационных информации? 11. Какое отношение имеет информационная ассоциация к единице количества информации – биту? 12. Как получается каждый бит информации? Сколько бит извлекается при поиске заданного объекта среди множества, содержащего 32 разных объекта.
|
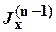x 1 = x n. Для описания основной информации чаще применяется именно такой вид. Например, для арифметической прогрессии имеем x 1 + (n - 1 ) d = x n.
