Определение, описание и средства анализа строя информационной цепи сообщений
В данном параграфе рассмотрены формализмы для определения, описания и анализа «геометрии расположения» элементов в конечных цепях сообщений произвольной природы. В отличие от исследований собственно знаковых последовательностей, отображающих цепи реальных сообщений, предлагается подход для анализа «строя цепи самого по себе», представляющего только взаимное расположение одинаковых и разных элементов цепи независимо от их обозначения, веса и содержимого. При рассмотрении информационных цепей сообщений разной природы, кроме прочего, отмечают их особое свойство, называемое порядком следования, взаимным расположением, построением или строем. Это неформальное понятие, в частности, неявно предполагает возможность выявления одинакового строя для некоторого (счетного) множества цепей сообщений с равной мощностью их составов (под событием здесь понимается выделенный элемент цепи). При этом состав последовательности определяется как мультимножество, элементами которого являются пары <символ, число его вхождений в данную последовательность>. Однако, по нашему мнению, из-за отсутствия формального определения объекта, представляющего «строй событий сам по себе», до настоящего времени не применяются математические средства, пригодные для описания и анализа взаимного расположения компонентов в конкретных цепях сообщений конечной длины. Поэтому затруднены или невозможны измерение и сравнение формы сигналов, рельефа изображений, композиции музыкальных произведений и речевых высказываний, порядка элементов в длинных молекулярных цепях и текстах, взаимного расположения элементов в массивах данных произвольной природы, размера и размерности. Представленные здесь положения основаны на понятиях, определениях и формализмах теории информации, разработанной М. Мазуром [2]. В рамках данной теории необходимо иметь в виду следующее. Любой кортеж конечной длины может рассматриваться как информационная цепь различных физических состояний, называемых сообщениями. Информационные цепи следует отличать от кодовых цепей сообщений, не являющихся носителями информации. Любая пара сообщений < x i, x j > данной информационной цепи связана особого типа преобразованием – информацией J xi,j. С учетом отмеченного в данном параграфе рассматриваются некоторые новые средства формального исследования и количественного описания структуры отдельной информационной цепи, сообщения которой представимы знаками [9]. Предлагаемый анализ осуществляется на основе формального объекта, представляющего только взаимное расположение компонентов цепи. Строй цепи определяется как особый кортеж, компонентами которого являются натуральные числа, представляющие знаки данной последовательности следующим образом: – при просмотре цепи слева направо каждый первый встречный отличный от других знак обозначается очередным натуральным числом, – повторные вхождения выделенного знака заменяются тем же числом. Для наглядности ниже представлены три разные знаковые цепи и два их строя.
Таким образом, строй представляет взаимное расположение различимых и одинаковых элементов цепи независимо от их обозначения, веса и содержимого. Полная неоднородная знаковая цепь представлена разложением однородных цепей, в которых отдельные позиции заняты одинаковыми знаками. Для примера ниже выделены две (j- я и l- я) однородные цепи из состава трехзнаковой неоднородной цепи.
1 2 3 2 3 3 3 2 1 3 2 1 2 1 3 3 2 полная неоднородная цепь 1 – – – – – – – 1 – – 1 – 1 – – – j - я однородная цепь – 2 – 2 – – – 2 – – 2 – 2 – – – 2 l - я однородная цепь 1 2 – – – – – – 1 – 2 1 2 1 – – 2 бинарно - однородная цепь
Число пустых позиций (плюс один) между любыми (i и i +1) двумя ближайшими вхождениями выделенного знака j названо интервалом «времени» D ij. Конечный или единственный интервал определен до конца цепи. Каждая однородная цепь представлена вектором интервалов, а полная знаковая цепь – матрицей интервалов. Таблица 2.1
Числовые характеристики строя цепи
Сформулированы, представленные в табл. 2.1 (кроме 14, 15, 16), выражения для числовых характеристик, которые компактно описывают оригинальный порядок элементов цепи. Базовой характеристикой является абсолютный объемV j строя выделеннойj - йоднородной цепи, который определяется перемножением в порядке вхождения всех её интервалов Δ ij в виде (1). Логарифмирование представленных величин дает набор удобных для практики аддитивных информационных характеристик строя цепи [9,10,11]. В таблице обозначены: j – номер знака в алфавите или номер однородной цепи; D ij – интервал между i и i +1 вхождениями знака j в однородной цепи; logD ij – удаленность i+1 вхождения знакаj относительно его i вхождения; n j – число вхождения знака j в цепи; m – мощность алфавита знаков цепи; n – длина полной знаковой цепи, равная числу всех ее позиций; D aj, D gj – соответственно средний арифметический и средний геометрический интервалы j однородной цепи; V j – абсолютный объем строя j однородной цепи; G j – глубина расположения элементов j однородной цепи; logD gj – средняя удаленность знака j в однородной цепи; V – абсолютный объем знаковой цепи, рассматриваемой как композиция независимых однородных цепей; G – глубина расположения всех элементов цепи; D g – средний геометрический интервал строя знаковой цепи; D gm – средний геометрический интервал строя регулярной знаковой цепи; g – средняя удаленность любого элемента в знаковой цепи; D – число описательных информаций, используемых (по М. Мазуру) для определения некоторого знака цепи; I – число идентифицирующих информаций, используемых (по Мазуру) для распознавания отдельного знака; t j – периодичность (следования элементов) j -ой однородной цепи;
dV j – нормированный объем строя j -ой однородной цепи; r – регулярность (следования элементов) знаковой цепи. Для виртуальной регулярной знаковой цепи, в которой все интервалы каждой однородной цепи равны D ij = D aj = n / n j, числовые характеристики строя цепи (10) и (11) записываются в табл.2.1 формулами Мазура (14) и (15), представляющими соответственно числа описательных и идентифицирующих информаций в цепи сообщений. Для бесконечной знаковой цепи (n ®¥) формула Мазура (15), в которой Для нерегулярных цепей формулы Мазура и Шеннона, в которых при подсчете информации не учитывается порядок элементов, дают оценку строя цепи только «сверху», т.к. (D g / D) £ 1, g £ H. (2.36), (2.37)
Таким образом, полученные формулы в определенном смысле обобщают известные формулы Шеннона и Мазура для количества информации, т.к. в отличие от последних учитывают не только мощность состава знаковой цепи, но и взаимное расположение ее элементов. В дополнение к распределению частот вхождения знаков { P j } полное описание строя символьной цепи представлено распределением средних удаленностей элементов ее однородных цепей {logD gj } или величин { G j }, где j =1, 2, …, m (см. рис. 2.4б, 2.5д). Компьютерные эксперименты и сравнительный анализ знаковых цепей показывают высокую чувствительность предлагаемых характеристик относительно порядка элементов и его изменений в цепи (табл. 2.2).


  Таблица 2.2 Числовые характеристики порядка элементов в массивах данных разной природы
Вопросы для закрепления и углубления материала 1. Определите полезную, избыточную и паразитную информации и приведите их примеры. 2. Что такое описательная информация? Каково назначение исходного сообщения и исходной информации и какими они могут быть? 3. Определите понятие «редкость». 4. Определите полную описательную информацию множества сообщений информационной цепи; приведите примеры таких информации. 5. Приведите соотношения для определения числа описательных информации следующих информационных цепей: 1) состоящей только из разных сообщений, 2) содержащей основную информацию, 3) содержащей группы одинаковых сообщений. Докажите справедливость приведённых соотношений. 6. Что такое идентификация? Что может быть критерием выделения сообщения? На каком утверждении основана идентификация сообщения? Каково число вопросов или выборов возможно при идентификации сообщения? 7. Что такое идентифицирующая информация и каково её отличие от описательной информации? 8. В какой информационной цепи возможна однозначная идентификация? 9. Приведите соотношения для определения числа идентифицирующих информаций в информационной цепи, состоящей только из разных сообщений, а также – содержащей группы одинаковых сообщений; докажите справедливость приведенных соотношений. 10. Какова зависимость между числом описательных и идентифицирующих информаций? 11. Почему идентифицирующих информаций меньше, чем описательных в данной информационной цепи? 12. Какова связь между соотношением для определения числа идентифицирующих информации и формулами Р. Хартли и К. Шеннона? 13. Какие количественные характеристики информационной цепи определяет среднее число описательных информаций? 14. Какова связь между энтропией и разнообразием описательных информации в различных информационных цепях? 15. Укажите области явлений, где целесообразен подсчёт описательных и идентифицирующих информации? 16. Понятия однородной и неоднородной информационных цепей сообщений. 17. Определения интервала и удаленности выделенного сообщения в однородной цепи. 18. Понятие и определение строя информационной цепи сообщений (в отличие от собственно информационной цепи сообщений). 19. Приведите числовые характеристики строя информационной цепи сообщений. 20. Каким образом связаны числовые характеристики строя цепи сообщений с формулами для количества информации М. Мазура и К. Шеннона?
|
















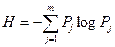

 –средний геометрический объем строя однородных цепей,
–средний геометрический объем строя однородных цепей,


