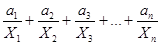Регрессионный анализ
Корреляционно-регрессионный анализ предполагает установление аналитической формы связи (регрессионный анализ) и измерение тесноты, направления связи (корреляционный анализ). Наиболее часто для характеристики регрессии используют следующие типы функций: Линейная регрессия Ух = а0 + а1Х или У1, 2,3 …п = а0 + а1Х1 + а2Х2 + … + апХп Параболическая связь Ух = а0 + а1Х + а2Х2 или У1, 2, 3…п = а0 + а1Х12 + а2Х22 + … + апХп2 Гиперболическая связь Ух = а0 + а1 Полулогарифмическая кривая Ух = а0 + а1lg Х Логистическая кривая Ух = Показательная функция Ух = а0а1Х или У1, 2, 3…п = еА0 + А1Х1 +А2Х2 + … АпХп Степенная функция Ух = а0Ха1 или У1, 2, 3,…п = а0Х1А1· Х2А2 · Х3А3….ХпАп Оценка параметров уравнений регрессии (а0, а1, а2…ап) осуществляется методом наименьших квадратов. Сущность его заключается в минимизации суммы квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии. Каждый коэффициент регрессии показывает, на сколько в среднем изменится величина результативного признака в случае изменения факторного признака на единицу при фиксированном положении остальных факторов. Значимость коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:
входные параметры: α, ν = п – к - 1, Если tфакт > tтабл, то параметр модели принимается значимым где σ2аi – дисперсия коэффициентов регрессии; α – уровень значимости критерия о равенстве нулю параметров; ν – число степеней свободы; п - количество единиц совокупности; к – число факторных признаков в уравнении; Адекватность корреляционно-регрессионной модели осуществляется с помощью F- критерия Фишера:
входные параметры: α, ν1 = к, ν2 = п-к-1, где r2УХ – коэффициенты детерминации. Если Fфакт > Fтабл, то можно утверждать о надежности построенного уравнения. Для характеристики корреляции применяют показатели тесноты связи между явлениями. Они различаются в зависимости от формы и вида связи.
|

 или У1, 2, 3…п = а0 +
или У1, 2, 3…п = а0 +