Краткие сведения из теории
Критерии качества приема определяют правила построения оптимальных приемников и для модулированных сигналов. При гауссовской помехе критерий Котельникова (идеального наблюдателя) может быть представлен неравенством (1.4). Усредним по времени (проинтегрируем) показатели степеней:
После несложных преобразований это выражение можно записать в ином виде:
где q(Si) = ESi = Приведенные выражения позволяют сформировать структурную схему оптимального приемника, она должна содержать звенья, с помощью которых получаются две функции для каждого сигнала. Далее должно быть решающее устройство, которое определяет, по какой из ветвей обработки имеется максимальный результат, и тому сигналу отдается предпочтение в решении. Это положение иллюстрируется схемой, приведенной на рис. 3.1. Более определенный вид оптимального приемника будет зависеть от вида принятых сигналов [1 - 4].
Рис. 3.1. Структурная схема оптимального приемника
Рассмотрим демодулятор амплитудно-модулированных сигналов: S0 = 0, S1 = A0cos w0t (рис. 3.2).
В итоге получается так, что оптимальный приемник должен анализировать неравенство, которое следует из (2.6):
или
В результате этого анализа схема, приведенная на рис. 3.1, упрощается и принимает вид, приведенный на рис. 3.3.
Рис. 3.3. Оптимальный демодулятор при амплитудной модуляции
Первые два блока приемника – это коррелятор; полученное значение взаимной корреляции сравнивается с порогом
Так как энергии сигналов равны (Е0 = Е1), то неравенство (3.2) упрощается, и критерий проверки сводится к сравнению двух функций корреляции:
Таким образом, на этих двух примерах мы выяснили, что структура приемника зависит от системы применяемых сигналов. Но их вид в системе связи определяет не только это, но и помехоустойчивость системы связи. Различить при приеме сигналы S0 = 1 В и S1 = 1,1 В приемнику сложнее, чем сигналы S1 = 1 В и S0 = -1 В. Вероятность ошибки как основная характеристика помехоустойчивости будет зависеть не только от интенсивности помех, но и от вида сигналов. Прежде чем сделать какое-то заключение, проведем анализ вероятности ошибки оптимального приемника. Одним из критериев помехоустойчивости является вероятность ошибочного приема бита рош, которая зависит от отношения сигнал/помеха и определяется следующим образом: Рош = 1 – F(x), (3.7)
где F(x) = х – аргумент функции. В зависимости от вида модуляции аргумент х принимает различные значения: х = Из этих соотношений видно, что наибольшая вероятность ошибки получается при АМ, а наименьшая – при ФМ. Более подробно теоретические сведения о помехоустойчивости демодуляторов даны в [3, 4]. Приведенные выше схемы и теоретические выводы справедливы для когерентных приемников, при формировании которых имеются точные сведения о параметрах передаваемых сигналов – амплитуде, фазе, частоте. Такая ситуация характерна для многих каналов проводной связи, однако нередко фазу приходящего сигнала точно оценить не удается. Приемник, построенный в предположении, что начальная фаза приходящего сигнала неизвестна и может принимать любое значение на интервале 0 – 2π, называется некогерентным. В этом случае сравниваются не функции правдоподобия, а их математические ожидания, которые позволяют усреднить эти функции по всем возможным значениям фазы:
После преобразований это выражение можно представить так:
(3.9)
Полученное соотношение позволяет формировать обобщенную структурную схему некогерентного приемника, она должна иметь две ветви – для двух частей неравенства, в каждую из которых следует включить согласованный фильтр и амплитудный детектор. Напряжения на выходах фильтров Ф1 и Ф2, согласованных с сигналом, соответствуют интегралам неравенства, т. е. пропорциональны функциям взаимной корреляции; амплитудный детектор Д выделяет огибающие (модули) этих функций. Обобщенная структурная схема может быть конкретизирована для различных методов модуляции подобно тому, как это было сделано для когерентного приемника. В общем случае некогерентный метод приема дает большую вероятность ошибки, чем когерентный, но конкретные соотношения зависят от вида сигнала и свойств канала.
Обобщенная структурная схема некогерентного приемника приведена на рис. 3.5.
Рис. 3.6. Обобщенная структурная схема некогерентного приемника
|

 (y-S0)2/2σ2. (3.1)
(y-S0)2/2σ2. (3.1)
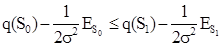 , (3.2)
, (3.2) – взаимная корреляция между принимаемым (y) и передаваемым (Si) сигналами;
– взаимная корреляция между принимаемым (y) и передаваемым (Si) сигналами;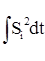 – энергия передаваемого сигнала.
– энергия передаваемого сигнала.


 . (3.3)
. (3.3)
 0 (3.4)
0 (3.4)

 . (3.5)
. (3.5)
 ). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным.
). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным. Разберем структуру частотного демодулятора: S0 = Scоsw0t; S1 = Scоsw1t (см. рис. 3.4).
Разберем структуру частотного демодулятора: S0 = Scоsw0t; S1 = Scоsw1t (см. рис. 3.4).

 . (3.6)
. (3.6) Смысл функции корреляции состоит в оценке статистической связи между сигналами. Естественно, с каким из двух сигналов «теснее» связан принимаемый сигнал, тому и должен отдать предпочтение приемник. Структурная схема оптимального приемника при частотной модуляции приведена на рис. 3.5.
Смысл функции корреляции состоит в оценке статистической связи между сигналами. Естественно, с каким из двух сигналов «теснее» связан принимаемый сигнал, тому и должен отдать предпочтение приемник. Структурная схема оптимального приемника при частотной модуляции приведена на рис. 3.5.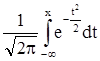 – функция Лапласа;
– функция Лапласа; при АМ; х =
при АМ; х =  при ЧМ; х =
при ЧМ; х =  при ФМ (если фазовый сдвиг составляет 180º), где E– энергия элементарного сигнала; N0 – спектральная плотность мощности шума.
при ФМ (если фазовый сдвиг составляет 180º), где E– энергия элементарного сигнала; N0 – спектральная плотность мощности шума. М[W(y/S1)] > M[W(y/S2)]. (3.8)
М[W(y/S1)] > M[W(y/S2)]. (3.8)





