Краткие сведения из теории. Любое приемное устройство, принимающее сигнал на фоне помех, можно представить структурной схемой
При линейном способе обработки, который используется для приема дискретных сигналов, результат обработки может быть представлен в следующем виде: Z(t) =
где φ(t) – временной функционал, определяемый методами обработки, в зависимости от которых классифицируются приемники. Если φ(t) = 1, то имеет место интегральный прием, при φ(t) = s(t) приемник является корреляционным, при φ(t) = cos ωt – синхронным детектором, а при φ(t) = s(t – τ) – автокорреляционным. В случае, когда φ(t) совпадает с импульсной характеристикой фильтра, приемник работает по принципу оптимальной фильтрации [1 – 3]. Основной задачей любого метода обработки сигнала является повышение соотношения сигнал/помеха. В данной лабораторной работе изучается первый из перечисленных методов – интегральный. Он в свою очередь может быть реализован как при непрерывной, так и при дискретной обработке (рис. 2.2).
а б
Рис. 2.2. Интегральный метод приема а – непрерывная обработка; б – дискретная обработка
Сигнал на выходе при дискретной обработке будет представлен так:
где Sh и xh – отсчеты сигнала и помехи; Н – количество отсчетов. Найдем отношение мощностей сигнала и помехи на выходе. Мощности наиболее объективно отражают их характеристики, так как дают представление о сигнале и времени его существования. Мгновенная мощность сигнала в момент его окончания
Если Найдем мощность случайной помехи и ее дисперсию. Для этого воспользуемся формулами статистики, известными из теории сигналов. Если помеха на входе и выходе имеет нулевое математическое ожидание, то
где Двойная сумма
Чем больше Н, тем больше выходное соотношение сигнал/помеха. Таким образом, интегральный метод увеличивает соотношение сигнал/помеха. Интегрирование сигнала при постепенном его наращивании показано на рис. 2.3. Помеха, так как она имеет знакопеременный характер, на выходе интегратора приближается к нулю (при условии
Рис. 2.3. Интегрирование сигнала и помехи
В случае, когда Δτ > Δt, в пределах одного импульса имеется статистическая связь между отсчетами помехи (что соответствует меньшей скорости ее изменения) и выигрыш в соотношении сигнал/помеха уменьшается.
|

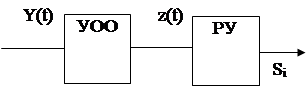
 Любое приемное устройство, принимающее сигнал на фоне помех, можно представить структурной схемой, приведенной на рис. 2.1, где УОО – устройство оптимальной обработки; РУ – решающее устройство; y(t) – аддитивная смесь полезного сигнала s(t) и помехи n(t) на входе приемника; Z(t) – результат обработки в УОО; Sί – решение в пользу одного из передаваемых сигналов.
Любое приемное устройство, принимающее сигнал на фоне помех, можно представить структурной схемой, приведенной на рис. 2.1, где УОО – устройство оптимальной обработки; РУ – решающее устройство; y(t) – аддитивная смесь полезного сигнала s(t) и помехи n(t) на входе приемника; Z(t) – результат обработки в УОО; Sί – решение в пользу одного из передаваемых сигналов. 
 , (2.1)
, (2.1)
 , (2.2)
, (2.2) . (2.3)
. (2.3) , т. е. сигнал постоянен во времени, то
, т. е. сигнал постоянен во времени, то  .
. (черта сверху означает усреднение). Квадрат суммы можно представить следующим образом:
(черта сверху означает усреднение). Квадрат суммы можно представить следующим образом: , (2.4)
, (2.4)
 по смыслу является взаимной корреляцией между двумя отсчетами помехи, т. е. автокорреляционной функцией (АКФ). Если интервал корреляции помехи Dt меньше временного шага дискретизации Dt, то статистическая связь отсутствует и данная величина равна нулю. Таким образом, при условии статистической независимости отсчетов помехи отношение мощностей сигнала и помехи
по смыслу является взаимной корреляцией между двумя отсчетами помехи, т. е. автокорреляционной функцией (АКФ). Если интервал корреляции помехи Dt меньше временного шага дискретизации Dt, то статистическая связь отсутствует и данная величина равна нулю. Таким образом, при условии статистической независимости отсчетов помехи отношение мощностей сигнала и помехи . (2.5)
. (2.5) ).
).



